Introduction
Most individuals show a preference for use of one hand or the other for both activities of daily living and specialized skills such as playing an instrument. Skill training for sport is often highly lateralized to the preferred hand, especially for those skills which require a high degree of fine motor control such as dart throwing, pitching, and shooting. Traditionally, inventories of hand preference for a set of tasks have been used to define handedness or hand dominance (Bryden, 1977; Oldfield, 1971). Handedness inventories indicate about 90% of the population is right-hand dominant, and left-hand dominant individuals indicate preference for the non-dominant arm more frequently than right-hand dominant individuals (Borod et al., 1984). A traditional view, a global dominance hypothesis, which emerged from much of this work, posited that the dominant arm is superior to the non-dominant arm in all aspects of control. However, more thorough investigation of inter-limb differences in motor behavior has led to a competing hypothesis that the dominant and non-dominant limb may show different specialization (Woytowicz et al., 2018). The dynamic-dominance hypothesis of motor lateralization (Sainburg, 2002), suggests that in right-hand dominant individuals the dominant right arm is specialized for predictive control of dynamics to produce smooth and efficient movements, whereas the non-dominant left arm is specialized for stability to unanticipated perturbations (Sainburg, 2005). Subsequent work showed the dynamic dominance hypothesis holds for left-hand dominant individuals, however limb specialization asymmetry was decreased primarily due to greater predictive control of dynamics on the non-dominant arm than is typical in right-hand dominant individuals (Przybyla et al., 2012). There is now a wealth of behavioral evidence in support of the dynamic-dominance hypothesis (for review, Sainburg, 2014), however, the neural underpinnings of motor lateralization and handedness are less clear (Andersen and Siebner, 2018).
The investigation of modularity in muscle co-activation has aided our understanding of motor control and motor pathology (Andersen and Siebner, 2018), yet has been sparsely used in the study of handedness. A long-standing hypothesis in motor control questions whether dexterous coordination of a musculoskeletal system with numerous redundant degrees of freedom (Bernstein, 1967; Latash, 2012; Tresch and Jarc, 2009; Tresch et al., 1999) may be simplified through the co-activation of specific groups of muscles that form basis sets, commonly referred to as muscle synergies, from which complex actions can be assembled (for review, Bizzi and Cheung, 2013; Bizzi et al., 1991; Tresch and Jarc, 2009). Though criticisms of this thesis have been put forward, such as for example that synergies may be artifacts of the musculoskeletal constraints of the limb or biomechanical constraints of the task (Kutch and Valero-Cuevas, 2012), the use of muscle synergies to describe and compare fixed regularities in muscle activation remains a valuable tool for the study of motor control and has been widely applied across species and tasks.
The limited research testing for differences in synergistic co-activation of muscles of the upper limb, as a function of handedness, have primarily focused on the shoulder and elbow during whole arm movements. In the most rigorous comparison of dominant and non-dominant upper limb synergies to date, left and right arm shoulder and elbow muscle synergies were extracted during a center out reaching task under different load conditions in 41 right-handed healthy individuals (Pellegrino et al., 2020). Results indicated a high degree of synergy similarity between the limbs across all force conditions, despite significant differences in muscle activation, suggesting differences in the activation of motor modules but invariance in module structure. In a second study, inter-limb differences in shoulder and elbow muscle synergies were extracted during a whole arm isometric force task in healthy right handed individuals, as control comparison to assess differences in the affected and unaffected limbs of individuals with hemiparesis due to stroke (Roh et al., 2013). Results indicated a high degree of similarity not only between the right and left limb, but also between participants in the sample. In a study that included both left- and right-hand dominant individuals, Duthilleul and coworkers (Duthilleul et al., 2015) observed that the number of upper limb muscle synergies observed during circular arm movements were similar between dominant and non-dominant limbs but different between left- and right-hand dominant individuals for gross movements (wide circles). In contrast, finer movements (smaller circles) were associated with higher number of synergies for dominant arm, but no difference between left- and right- handed individuals. Notably, this is the only study to include muscles of the forearm in analysis.
The above-mentioned work has set a foundation for understanding patterns of muscle co-activation associated with handedness in the proximal upper limb. However, it is well-known that the corticospinal control of the proximal upper limb is different from that of the distal upper limb. For example, there is a greater density of minimally divergent monosynaptic corticospinal projections to the alpha motor neurons that innervate the intrinsic hand muscles compared to those alpha motor neurons that innervate the proximal muscles of the upper arm (Rathelot and Strick, 2006; Rathelot and Strick, 2009; Zaaimi et al., 2018). Therefore, it cannot be assumed that findings relating muscle synergies and handedness for the proximal limb would also be found in the distal limb and hand. In this investigation we specifically tested the similarity of hand muscle synergies between the non-dominant and dominant arm of right-handed and left-handed individuals. EMG data were extracted from voluntary movements in the American Sign Language posture set. This task provides wide variability of hand postures and finger individuation and has previously been used for hand synergy investigation (Ajiboye and Weir, 2009). Comparisons of synergies were made between the limbs of each individual to test for differences in inter-limb synergy similarity between left- and right-hand dominant individuals, and between limbs of all individuals in order to describe limb-specific synergy similarity across the sample population.
Methods
Participants
Ten young healthy participants with no known history of neurological disease participated following informed consent in accordance with the Institutional Review Board of Northeastern University. Five participants were right-hand dominant (27.8 ±8.0 years old) and five participants were left-hand dominant (22.8 ±3.6 years old) according to the Edinburgh Handedness Inventory (Oldfield, 1971).
Electromyography
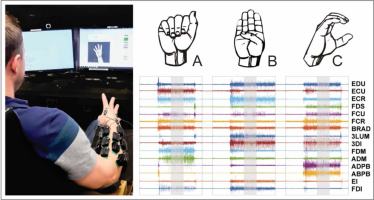
Surface EMG (Trigno, Delsys Inc. Natick, MA, USA) was recorded from 15 muscles: 1st dorsal interosseus (FDI), extensor indicus (EI), 3rd dorsal interosseous (3DI), 3rd lumbrical (3LUM), adductor pollicis brevis (ADPB), abductor pollicis brevis (ABPB), abductor digiti minimi (ADM), flexor digiti minimi (FDM), flexor carpi radialis (FCR), flexor carpi ulnaris (FCU), flexor digitorum superficialis (FDS), extensor digitorum (EDC), and extensor carpi radialis (ECR), extensor carpi ulnaris (ECU), brachioradialis (BRD). All EMG data were sampled at 1000Hz.
Experimental Task
Data were acquired for the right and left limbs in two separate sessions, less than one week apart. Participants were seated with the elbow supported and wrist free to move. In each session, participants shaped their hand into letters and numbers of the American Sign Language (ASL) posture set (Fig. 1) presented as pictures on a computer screen (33 postures, 3 repetitions, 99 trials). Dynamic letters ‘J’ and ‘Z’ were omitted, along with the number “0”, which is visually the same as the letter “O”. For each character, participants were given two seconds to form the posture, six seconds to maintain it, and two seconds to return to the relaxed starting posture. Participants were instructed to form each pose with sufficient force to maintain the posture as if they were signing to someone seated across from them. Participants were specifically instructed to limit motion at the elbow during posturing. All participants were naive to ASL prior to participation.
EMG Processing & Synergy Extraction
All data processing was performed offline using custom analyses in Matlab (Mathworks Inc.). EMG data (size m, muscles) from each ASL pose (p) was filtered with a zero phase fourth order Butterworth bandpass filter with cutoffs at 10Hz and 300Hz. The mean absolute value (MAV) of the filtered EMG within a 2 second time window (5.5 – 7.5 sec from trial start) was determined for each muscle and normalized to the corresponding muscle’s within trial maximum activation. The time window for MAV extraction was chosen to capture steady state activation associated with maintenance of the pose. Data for each pose across all trials were concatenated into a matrix [size: muscles (15) x poses (99)] for each hand individually.
Non-negative matrix factorization (Lee and Seung, 1999) was used to extract muscle synergies and their corresponding activation coefficients from the recorded muscle activity. For a preselected rank (N) representing the number of synergies to be included, EMG matrices (M) were factorized into a synergy matrix (B, size m x p) containing a linear combination of time invariant non-negative vectors and an activation matrix (A, size p x N) containing the pose-dependent nonnegative activation coefficients of each synergy (Equation 1).
The extracted synergies (B) reflect the spatially fixed regularities (Kargo and Giszter, 2008; Safavynia and Ting, 2012) in muscle groupings that are common across the formation of different poses. NMF finds B and A by minimizing the squared norm of the residual (ε), under the assumption that it follows a Gaussian distribution that is zero mean and uncorrelated. The algorithm iteratively updates the model parameters until the squared norm of the residual changes by less than 0.001 over ten iterations.
To select the rank (N) to be used in subsequent analysis, the NMF process was repeated 10,000 times (in order to increase the likelihood of the NMF approximating the global minima) for each possible number of synergies 1 to 15 (the number of muscles examined).
For the best fit run at each rank, the proportion of variance explained by the model (R2) was determined as described in Equation 2, where SSE is the sum of squared error, SST is the total sum of squares, subscripts (i,j) denote the corresponding entry of M, and is the average over all entries of M (Devarajan and Cheung, 2014). Rank N for subsequent analysis was chosen as the minimum number of synergies needed to reconstruct 90% of the variance in the data from which they were derived (R2 ≥ .90). This methodology has been used extensively for the purpose of deriving a low dimensional representation of synergistic muscle activation (Duthilleul et al., 2015; Sawers et al., 2015; Tresch et al., 2006; Tresch and Jarc, 2009), and has been described by our group previously (Günay et al., 2019; Jacobs-Skolik et al., 2020).
Quantification of Similarity Between Synergies
To compare individual synergies between different hands, dot products were computed between all possible pairs of synergies (one from each hand), and a greedy search procedure was used to define matching pairs. The best-matching pair was defined as the one with the highest dot product; this pair was removed, and the next best matching pair was selected as the highest dot product among the remaining synergy pairs. This process continued until there were no more unpaired synergies left in the set of lower rank (Tresch et al., 1999). If rank differed between sets, the set with the higher rank was left with an unmatched synergy(ies). A similarity index (SI) describing the global similarity in synergistic muscle activation was determined by averaging the dot products for the chosen pairings.
Statistical Design
To assess differences in the number of synergies required to achieve R2 ≥ .90 between hands [Right Dominant Right Hand (RD-RH), Right Dominant Left Hand (RD-LH), Left Dominant Right Hand (LD-RH), Left Dominant Left Hand (LD-LH)], we conducted a 2-way ANOVA with factors of Dominance (RD, LD) and Side (RH, LH). To compare synergy similarity of the right hand and left hand (RH & LH pairs) between RD and LD participants, an independent samples t-test was used to test for differences in SI. To assess differences in synergy similarity associated with side or dominance between RD and LD individuals, we determined the SI of synergy pairs made from each hand of LD participants to each hand of RD participants. Separate independent samples t-tests were used to test for differences in SI between right (RD-RH & LD-RH) and left hands (RD-LH & LD-LH), and between dominant (RD-RH & LD-LH) and non-dominant hands (RD-LH & LD-RH). Each comparison group (i.e. RD-RH & LD-RH) contained values from 25 hand pairs. Similarity of hand specific synergies across participants was determined by obtaining SI values of synergy pairs made from matching all hands of the same type (i.e. every RD-RH hand to every other RD-RH). This procedure yielded a total of 10 unique pairs excluding pairing any hand to itself. Differences in the similarity of hand specific synergies (RD-RH, RD-LH, LD-RH, LD-LH) were tested using a 2-way ANOVA with factors of Dominance (RD, LD) and Side (RH, LH). Alpha values for all tests were set to .05. Post-hoc tests with correction for multiple comparisons were applied where main effects or interactions were found to be significant. All statistical analyses were conducted using SPSS (version 20; SPSS, Chicago, IL).
Results
Across all participants and all arms 8.7 ±1.0 (range: 8-11) synergies were required to reconstruct the original EMG data at R2 ≥ .90 (Table 1, Fig. 2). On average a greater number of synergies were observed for LD participants, however a 2-way ANOVA with factors Hand (RH, LH) and Dominance (RD, LD) indicated no significant main effect of Hand (F1,16 = 3.459, p = .081), or Dominance (F1,16 = 0.00, p = 1.000), and no Hand x Dominance interaction (F1,16 = 0.216, p = .648).
Figure 2
Left. Participant mean (±sd) reconstruction (R2) for each hand for ranks (1-15). R2 increases monotonically with increased rank. Right. Number of muscle synergies required to reconstruct task EMG data satisfying R2 ≥ .9.
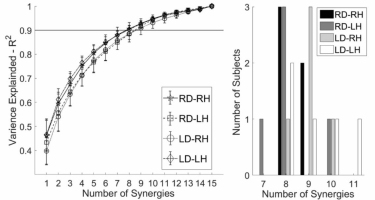
Table 1
Number of muscle synergies required to reconstruct task EMG data satisfying R2 ≥ .9 for each hand tested.
| S1 - LD | S2 - LD | S3 - LD | S4 - LD | S5 - LD | Mean | |
|---|---|---|---|---|---|---|
| LH | 11 | 8 | 8 | 10 | 9 | 9.2 |
| RH | 10 | 9 | 8 | 9 | 9 | 9 |
| S6 - RD | S7 - RD | S8 - RD | S9 - RD | S10 - RD | ||
| LH | 10 | 8 | 8 | 8 | 7 | 8.2 |
| RH | 8 | 8 | 8 | 9 | 9 | 8.4 |
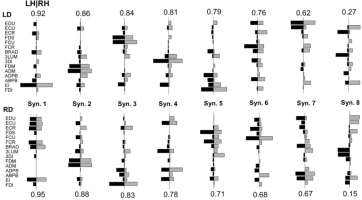
Matched pairs of LH & RH synergies for an example left-hand dominant participant and right-hand dominant participant are shown in Figure 3. The SI between LH & RH synergies for LD participants was .77 ± .05 (range: .70 - .83), and for RD participants was .74 ± .06 (range: .66 - .83). No significant difference in SI of the RH & LH was observed between LD and RD participants (t8 = .660, p = .528).
Figure 3
Greedy search matched left hand (black) and right hand (gray) synergy pairs for a left hand dominant (LD, top, participant 3), and a right hand dominant (RD, bottom, participant 8) participant. Numbers above or below synergy pairs indicate the pairwise dot product.
Specific comparisons of similarity index (SI) between LD and RD participants were used to assess differences in synergy similarity between the left-hand (LD-LH & RD-LH) and right-hand (LD-RH & RD-RH), and differences in synergy similarity between dominant (LD-LH & RD-RH) and non-dominant hand (LD-RH & RD-LH). SI of left hands (.75 ± .05, range: .63 -.85) was significantly greater (t8 = 2.85, p = .006) than SI of right hands (.70 ± .05, range: .60 -.80). In contrast, SI of non-dominant hands (.72 ± .05, range: .66 - .89) was not significantly different (t8 = 2.85, p=.006) than SI of dominant hands (72 ± .06, range: .62 -.82), see Fig. 4.
Figure 4
Similarity indexes showing comparison between every arm used in the study. Hotter colors indicate a higher similarity index signifying greater similarity of synergies between paired arms. Boxes indicate group comparisons. Within arm analysis of LD-LH is highlighted in blue to draw attention to the comparatively high similarity of limbs within this grouping.
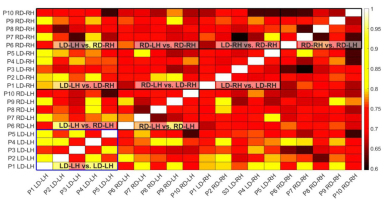
Hand specific SI across participants was found for LD-LH (.79 ± .06, range: .73 -.88), LD-RH (.71 ± .03, range: .68 -.75), RD-LH (.73 ± .05, range: .65 -.80), and RD-RH (.69 ± .06, range: .62 - .77). A 2-way ANOVA to test for differences in hand specific SI indicated a significant main effect of Hand (F1,36 = 13.746, p = .001), and a significant main effect of Dominance (F1,36 = 10.055, p = .003), but no Hand x Dominance interaction (F1,36 = 1.815, p = .186). Post-hoc independent samples t-tests with Bonferroni correction for multiple comparisons (.05/6 = .008) indicated significant differences in population level synergy similarity between LD-LH & RD-RH (t18 = -4.112, p < .001) and between LD-LH & LD-RH (t18 = -3.882, P = .001), and a trend level difference between LD-LH & RD-LH (t18 = -2.963, P = .008).
Discussion
In this study we examined whether limb dominance and side are associated with specific temporally invariant patterns of muscle co-activation during volitional movement. Unlike prior investigations which focused on the proximal upper limb (Duthilleul et al., 2015; Pellegrino et al., 2020; Roh et al., 2013), we focused on the intrinsic and extrinsic hand muscles of the distal upper limb and used a task that required a relatively high degree of finger individuation.
Our data reveals two main findings. First, that similarity of hand muscle synergies among left hands (across LD and RD individuals) was greater than that of right hands. Second, synergy similarity in the sample population was greater for the LD-LH case than the other hands tested (LD-RH, RD-LH, RD-RH). Unfortunately, only one of the three previous studies that compared synergies between the limbs tested both LD and RD individuals, limiting our ability to make direct comparisons to prior work. Duthilleul and colleagues (Duthilleul et al., 2015) reported two main findings regarding synergy composition between the limbs as a function of handedness. For gross movements of the arm (wide circle drawing), LD individuals showed greater synergy complexity (more synergies) than RD individuals, though no difference in synergy complexity was noted between the dominant and non-dominant limbs. In contrast, for finer-grained movements (small circles) the LD-LH showed lower complexity than other arms tested. These results are in contrast to the results of the present study where a greater, though not statistically significant, number of synergies was observed for the LD-LH condition compared to other hands, perhaps indicating differences between proximal and distal LD-LH synergies. Despite this difference, our study and that of Duthilleul both seem to depart from evidence suggesting similar behavior of the dominant hand in LD and RD individuals, and less asymmetry of limb specialization in LD individuals (Dassonville et al., 1997; Oldfield, 1971; Przybyla et al., 2012).
Quantitative analysis of limb kinematics in LD individuals has shown that reduced limb asymmetry is primarily due to greater dominant limb-like behavior of the non-dominant limb (Przybyla et al., 2012). It has been suggested that greater recruitment of ipsilateral motor cortex resulting in more symmetrical activation of the hemispheres, may be the neurological substrate of reduced behavioral asymmetry in left hand dominant individuals (Dassonville et al., 1997). However, whether these results reflect a consequence or cause of handedness remains an active research topic (Andersen and Siebner, 2018). Furthermore, we know of no study that has specifically looked at population variability of limb-specific behavior or hemispheric activation asymmetry in left- and right-handed individuals. We therefore offer a speculative explanation as to why in this study LD-LH synergies appeared to be more invariant in the population than synergies of other limbs. One possibility is that population invariance of LD-LH synergies results from the demands imposed on left-hand dominant individuals to use their left hands in the context of environments designed mainly for right-handed users. Given that most objects we interact with require right-handed manipulation, the left hand of left-hand dominant individuals, despite being specialized for predictive control per the dynamic-dominance hypothesis, may be forced into a stabilization role during bimanual activities, allowing the right hand to manipulate the object (Przybyla et al., 2012). Extended practice in a motor skill, for example a musical instrument, can shape muscle co-activation patterns, in essence creating use-dependent specialization of synergies (Gentner et al., 2010). It is possible that more varied use of the left hand by left-hand dominant individuals manifests in a more generic set of synergies than is seen in other limb-dominance combinations, thereby explaining greater similarity of LD-LH synergies within the population. However, the existence of a causal relationship between use-dependent neural reorganization and greater symmetry of hemispheric activation is still unknown (Andersen and Siebner, 2018).
As previously stated, our results did not reveal significant differences between the non-dominant and dominant limb at the individual or population level, in contrast to what might be expected from kinematic analyses showing specialized roles for the dominant and non-dominant limb as postulated in the dynamic dominance hypothesis (Sainburg, 2002; Sainburg, 2005). This result is in general agreement with previous investigations of the inter-limb synergy similarity of proximal upper limb muscles (Pellegrino et al., 2020; Roh et al., 2013), despite several reasons to suspect differences between the proximal and distal limb. Foremost, the degree to which the dynamic dominance hypothesis, which has mainly been predicated on experiments involving reach movements, holds for movement of the fingers remains unclear. A study of isometric finger force production and force stabilization supports the idea that the dominant limb may be specialized for adjustments to performance variables, however no evidence was found for non-dominant specialization for stabilizing steady-state isometric forces, as would be predicted by dynamic dominance (Zhang et al., 2006). While conclusions from a study of isometric force production may not be transferable to movements such as those used in the present study, the study by (Zhang et al., 2006) provides grounds for likely differences in inter-limb synergy similarity between proximal and distal limb segments.
Differences in the neurophysiological substrates of proximal and distal limb control, when viewed in the context of cortical differences associated with motor lateralization and handedness, provide a second reason to hypothesize that inter-limb synergy similarity may differ between the upper-arm and hand. It is well established that the alpha motor neurons innervating the distal upper-limb and hand receive a greater density of less divergent, monosynaptic, corticospinal projections than those synapsing onto motor neurons controlling the proximal limb, which often involve spinal interneurons (Rathelot and Strick, 2006; Rathelot and Strick, 2009; Zaaimi et al., 2018). Though some evidence in support of cortical synergies exists (Leo et al., 2016), it is spinal interneurons that have been consistently identified as an origin of synergistic muscle activation (Bizzi and Cheung, 2013; Hart and Giszter, 2010). However, differences in spinal anatomy and physiology are sparsely discussed in relation to handedness, and handedness is generally approached in the literature as something that is cortical in origin (Andersen and Siebner, 2018). Indeed, evidence indicating that fine motor control of the hand is dependent on direct projections from the contralateral motor cortex (M1) to spinal motorneurons (Lawrence and Kuypers, 1968; Muir and Lemon, 1983) has fueled hypotheses that handedness is reflected in the functional and structural hemispheric asymmetries in M1 (for a review, Andersen and Siebner, 2018; Goble and Brown, 2008; Hammond, 2002). Investigations have typically focused on handedness-related asymmetries in M1 structure (Amunts et al., 1996), functional topography (Triggs et al., 1999; Volkmann et al., 1998), activation during unilateral movement (Dassonville et al., 1997; Solodkin et al., 2001), cortical excitability (Brouwer et al., 2001; Ziemann and Hallett, 2001), functional connectivity (Pool et al., 2014), and effects of lesion due to stroke (Mani et al., 2014; Schaefer et al., 2009; Schaefer et al., 2012). Pellegrino and coauthors (Pellegrino et al., 2020) suggest the reason that differences in proximal upper-limb muscle synergies between arms were found only for synergy activation coefficients but not in number and structure of the muscle synergies themselves, is that the synergies observed are best attributed to muscle activation by spinal interneuron circuits. They do speculate that this finding may not hold for fine movements of the hand due to more direct cortical control. However, we did not find evidence that such a difference exists between dominant and non-dominant limb.
Several factors limit the interpretation of results in this study. First, the study was limited by a small sample size, though it was comparable to that of (Duthilleul et al., 2015). All participants reported to be naïve to ASL, however no history was taken on other forms of specialized mass practice with the hand, such as dart throwing, video gaming, or musical instrument playing. However, if such extreme skill specialization was present in our sample, it would have likely reflected as an outlier in the data, which was not the case. Finally, only a single task was used; therefore, it remains unknown whether synergies observed here were specific to the task or generalizable to a broader repertoire of hand function.
Here we investigated dexterous but not skilled movements. It has been suggested that the acquisition of new motor skills may involve the development of new muscle synergies, merging or fractionation of current synergies, or change their temporal activation (Asaka et al., 2008; Cheung et al., 2020; Frere and Hug, 2012). We hypothesize that a greater difference in muscle synergies between the dominant and non-dominant hand than was observed in this study may exist for individuals whose athletic training has created a large limb asymmetry for a highly specialized skill. Further examination into hand muscle synergies of left- and right-hand dominant individuals could improve training methods especially in sports that have high demands on precision in fine motor skills such as dart throwing, pitching, or e-sports where milliseconds can be the difference between a win or loss.