Introduction
The capacity to sense one’s own motion and force production is a pivotal feature to the success of motor tasks in any environment. Perpetually every meaningful task we complete involves action and perception of one’s body as well as the environment and its effects on the body. The tight coupling between action and perception has been studied in detail within the field of ecological psychology following the classical studies by Gibson (1979). In this paper, we review a theoretical approach to the neural control of movement, which interprets action-perception coupling as a natural consequence of the nature of human movements and their control.
Within this approach, neuroanatomical changes leading to alterations in properties of movement, including its stability, are expected to lead to changes in kinesthetic perception and its stability. In particular, disorders of the basal ganglia, which are traditionally described as movement disorders, have perceptual components that can be observed before any impairments are seen during clinical movement examination. We focus here on Parkinson’s disease (PD), which is one of the relatively widespread disorders of the basal ganglia caused by progressive degeneration of dopamine-producing neurons in the substantia nigra. As shown in a recent series of studies (reviewed in Latash and Huang, 2015), PD is associated with impaired control of action stability. By itself, this is also expected to lead to impairments in the stability of kinesthetic perception: indeed, a number of recent studies have documented impaired perception of force and position in PD (reviewed in Avanzino et al., 2018).
The review below progresses as follows. In the first section, Afferent And Efferent Components Of Kinesthetic Perception, the normative case for kinesthetic perception is introduced, including references to the neurophysiological elements contributing to the kinesthetic senses. The classical efferent copy concept is introduced and critically assessed. Further, we review briefly the theory of movement control with referent coordinates (RC), which is a recent development of the classical equilibrium-point hypothesis (Feldman, 1966, 1986; reviewed in Feldman, 2015). An original hypothesis on kinesthetic perception is introduced, notably with a modified concept of efferent copy. In the second section, Stability Of Action And Perception, the classical problem of motor redundancy (Bernstein, 1947/2020, 1967) is revisited, the principle of abundance (Gelfand and Latash, 1998; Latash, 2012) is introduced and linked to the uncontrolled manifold (UCM) hypothesis, and associated methods of analysis of movement stability (Scholz and Schöner, 1999; reviewed in Latash et al., 2007) are considered. Hypothetical neural mechanisms ensuring stability of salient performance variables by multi-element systems are defined as synergies. Further, this principle is extended to the perceptual realm, and the concept of iso-perceptual manifold (IPM, Latash, 2018) is introduced as a physiological framework for analysis of perceptual stability. In the third section, Problems With Action Stability in PD, problems with the neural control of action stability in PD and other neurological disorders are reviewed, and possible impairments of stability of kinesthetic perception are hypothesized. The fourth section, Kinesthetic Perception in PD, reviews the relevant literature regarding the behavior of PD patients in kinesthetic tasks, demonstrating support for a loss of stability in kinesthetic perception in PD. In the fifth section, Basal Ganglia and Synergies, the basal ganglia are hypothesized to be a crucial constellation of neural structures for synergies in action, perception, and possibly cognition; limitations are then enumerated.
Afferent and efferent components of kinesthetic perception
Accurate perception of body configuration and of one’s relationship to objects in the world is important for performing biologically meaningful movements. This is most clearly evidenced in the movements of individuals with large-fiber peripheral neuropathy (so-called “deafferented patients”): in the absence of nearly any information from peripheral sensory receptors, meaningful movements in the absence of vision become impossible and, even with vision, the joint coordination during arm movements becomes severely impaired (Sainburg et al., 1993).
The importance of efferent (i.e., related to control) signals for perception was demonstrated by a simple example by Helmholtz: saccadic eye movement produces the feeling of a stable world within which the eye moves. In contrast, a slight pressure to the side of the eye induces a mobile world around a stable self. The next important step was made by von Holst and Mittelstaedt (von Holst and Mittelstaedt, 1950) who introduced the concept of efferent copy, a copy of efferent signals participating in prediction of sensory consequences of the planned action and in the perceptual process. Reacting to the concept of reflex-initiated reactions to perturbation, von Holst and Mittelstaedt identified a paradox: how is it possible that walking could be initiated from a standing position without muscle reflex contributions resisting the apparent perturbation to the initial states of all the muscles (von Holst, 1954)? The authors concluded that afferent information could be classified into two types— reafference, the expected afferent feedback based on the efferent copy, and exafference, the afferent inflow produced by changes in the environment and, therefore, unpredicted by the efferent copy. This schema would permit an organism to differentiate between self-motion and imposed motion. Reafference was not expected to lead to changes in perception and contribute to reflex-based muscle reactions as long as it was compatible with the prediction based on the efferent copy.
Von Holst and Mittelstaedt associated efferent copy with a copy of signals generated by alpha-motoneuronal pools. This original idea has been criticized recently by Feldman (2009, 2016) who noticed that this formulation cannot explain muscle relaxation in animals after obtaining new postures: indeed, if all the relevant muscles are relaxed, the efferent copy is zero in both initial and final positions but muscle length values differ. These differences cannot be predicted by the efferent copy and hence have to lead to reflex-based activations. Since it is easy to relax at different body positions, the concept had to be revisited and modified (see later).
Afferent Components
The sensory receptors that participate in the kinesthetic senses have received a thorough review elsewhere (Proske and Gandevia, 2012); here, a cursory review will follow. The peripheral receptors that relay information on kinesthetic body states comprise an abundant set. These receptors include cutaneous and subcutaneous sensory endings, muscle spindle endings, Golgi tendon organs and joint capsule receptors.
Muscle spindles constitute an important source of kinesthetic information. Type Ia afferent fibers signal information from velocity- and length-sensitive endings, whereas type II afferent fibers carry information from length-sensitive endings only. The sensitivity of type Ia and type II fibers is modulated by gamma-motoneurons, which typically show co-activation with alpha-motoneurons thus contributing to coupling of efferent and afferent signals.
Golgi tendon organs have been traditionally viewed as tendon force sensors with segmental reflex effects on both parent muscle and its antagonist. A recent review of the sensory properties and inter-joint reflex patterns of Golgi tendon organs (Nichols, 2018) suggests that the set of information projected via Ib afferents has reflex effects on muscles controlling other joints of the extremity possibly contributing to patterns of inter-joint coordination.
Joint receptors, previously thought to be the primary source for joint position sense, have been identified to be active primarily at the extremes of the joint anatomical ranges (Ferrell et al., 1987) and do not constitute a crucial source of information on joint position as demonstrated, for example, by the unchanged joint position sense in persons after total joint replacement (Karanjia and Ferguson, 1983). Cutaneous and subcutaneous mechanoreceptors—organized between fast-adapting and slowly-adapting receptors—have been shown to augment illusory motion in muscle vibration studies with skin stretch (Collins et al., 2005). It is likely that cutaneous afferents represent an important source of information about body position (Proske and Gandevia, 2012).
It is evident that there are abundant sources of afferent information which can contribute to perception of variables such as joint position and force produced by an effector on the environment. This abundance may be viewed as functionally important, in particular contributing to robust percepts. Sensory signals, however, provide ambiguous information about local mechanical variables and have to be interpreted by the CNS with the help of ongoing efferent processes.
Efferent Component
The original equilibrium-point (EP) hypothesis (Feldman, 1966, 1986) describes the neural control of a muscle via changes in a control variable associated with the threshold of the stretch reflex (λ) set by varying subthreshold depolarizations of the alpha-motoneuronal pool.
Briefly consider the slow stretching of a single muscle from maximally shortened to maximally lengthened. The muscle will remain quiescent until its length reaches the threshold of the stretch reflex λ. With further stretch, the muscle force (and activation level) would increase with the difference between muscle length and λ. This produces a force–length curve such as those shown for three values of λ in Figure 1A. The particular length-force combination adopted by the muscle is addressed as the equilibrium point (EP), and is a function of both λ and the external load (three load characteristics are shown in Fig. 1A). Within this scheme, involuntary movements are produced by changes in the external load and voluntary movements are produced by changes in
λ.
Control at the joint level can be described by the setting of λ values for agonist and antagonist muscles (see
Note that, at the level of individual muscles, λ may be viewed as a referent coordinate (RC): removing the external load would lead to muscle movement towards λ. The recent generalization of the EP-hypothesis to multi-joint, up to whole-body, movements (reviewed in Latash, 2010; Feldman, 2015) suggests that movement of any effector is controlled by setting time changes in its RC. Further, a sequence of few-to-many mappings leads to RC(t) functions at the level of joints and muscles (illustrated later in Fig. 4).
Figure 1
Basics of the control with referent coordinates. A: At the level of the muscle, λ specifies the length threshold of the tonic stretch reflex. Changes in muscle length and force can occur from a shift in or from shifts in external load. A combination of force and length when the muscle is in equilibrium with the external load is addressed as the equilibrium point (EP), e.g., EP2B, with subscripts representative of λ and load. Afferent signals of various modalities increase in magnitude along the force-length characteristics. Efferent (EFF) command serves as a referent coordinate within which afferent (AFF) signals are interpreted to form perception of muscle length and force, symbolized as EFF + AFF. B: At the level of the joint, force-length characteristics for agonist and antagonist muscles are specified by their respective AG and ANT. The resultant torque-angle characteristic defines possible angle/torque combinations for the joint. C: At the level of the joint, the R-command results in a parallel shift in force-length characteristics, effectively moving the torque-angle characteristic without changing its slope.
D: The C-command represents shifts of the two force-length characteristics in opposite directions, effectively changing the slope of the torque-angle characteristic.
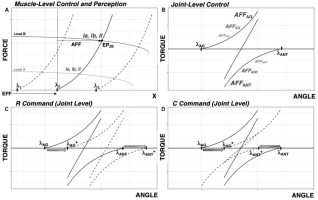
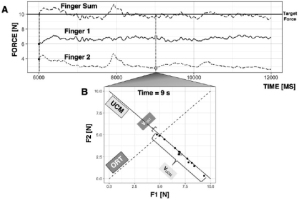
Figure 2
Synergies. A: A subject is shown an on-screen target and is asked to produce 10 N of force with two fingers of the right hand. B: Across trials, at each time point, Finger 1 force (F1) is plotted against Finger 2 force (F2). The space along which the performance variable remains unchanged (i.e., F1 + F2 = 10 N) is the uncontrolled manifold (UCM); the space along which performance changes is the orthogonal to the UCM space (ORT). Variance of the data within the UCM and within ORT space are graphically represented.
Kinesthetic Perception Within the Scheme of RC Control
Within the scheme of control with λ (or RC), signals from all major receptor groups increase with deviations along the force-length curve from (Figure 1B). This means that setting λ creates a system of coordinates for estimation of any of the available sensory signals in terms of mechanical variables, length and force, which are naturally linked by the force-length curve. A copy of λ (RC) participating in the perceptual process may be addressed as an efferent copy avoiding the aforementioned controversy with the original definition.
For example, to estimate muscle length, the CNS has to add the sensory signal to the efferent signal (λ) after conversion into commensurate units (Feldman and Latash, 1982a; Feldman, 2009). A similar process can be used for estimation of muscle force. For more functionally-relevant variables, perception of joint angle and torque can be associated with setting efferent commands (R- and C-commands, Fig. 1C,D) which translate into the coordinate and slope of the torque-angle characteristic. Sensory signals allow estimating deviations of the joint state from its RC defined primarily by R (the C-command can have an effect in cases of strongly asymmetrical agonist-antagonist muscle groups).
This scheme allows interpreting a number of perceptual phenomena including accurate perception of position across loading conditions (Feldman and Latash, 1982a), kinesthetic illusions induced by muscle vibration (Reschechtko et al., 2018), perceptual errors during unintentional force drifts (Abolins et al., 2020), and counterintuitive effects of agonist-antagonist co-activation on force perception (Cuadra et al., 2020).
Stability of action and perception
We define dynamical stability as an ability to return to an initial position or trajectory following small, transient external force perturbation. Given that multiple solutions exist, which satisfy completion of any natural task involving multiple effectors (limbs, joints, muscles and motor units), the capacity for biological movement to demonstrate dynamical stability is highly nontrivial.
Nikolai Bernstein (1967) addressed the presence of redundant degrees of freedom as the main problem of motor control. Recently, the inherent redundancy in kinematic and kinetic spaces satisfying task completion has been reformulated as abundance (Gelfand and Latash 1998; Latash, 2012): the available degrees of freedom in kinematic, kinetic, and muscle activation spaces afford biological movements the capacity to demonstrate both stability to frequent unexpected changes in the environment and body internal states, and flexibility – an ability to adjust an ongoing action without affecting salient performance variables.
Consider performing the task of producing 10 N of force on a surface by pressing with two fingers, as shown in Figure 2A. If the force of a digit increases, the other digit must decrease its force to stabilize total force (performance variable). In doing so, the fingers form a synergy: they compensate for each other’s errors (Latash, 2008).
If asked to perform this task a number of times in an experiment, the behavior across trials will show variability in two directions: in the direction of maintained task performance (sum of forces is 10 N) and in the orthogonal direction of altered task performance (sum of forces is not equal to 10 N). As illustrated in Figure 2B, the inter-trial variance in these directions can be quantified within the space where total force is constant (its uncontrolled manifold, UCM, Scholz and Schöner, 1999; Latash et al., 2007) and orthogonal to the UCM (labelled as ORT in Fig. 2B). For the two-finger system, the UCM is one-dimensional and is equivalent to a line along which the sum of finger forces is exactly equal to 10 N.
The UCM hypothesis provides a quantitative framework through which the stability of action can be measured with respect to some performance variable. The degree to which a system is organized into a synergy can be quantified by comparing inter-trial variance along the UCM and along ORT, VUCM and VORT, both quantified per degree of freedom. For a performance-stabilizing synergy, VUCM > VORT is expected. Sometimes, the two variance indices are reduced to a single index – synergy index - ΔV computed as the normalized difference between VUCM and VORT.
Note that having a strong synergy stabilizing a salient variable may be useful during steady-state tasks but it may be counterproductive when the salient variable has to be changed quickly. The CNS has an ability to modify stability of an ongoing action in preparation to quick actions. This ability is represented as: (1) a drop in the synergy index during steady-state in conditions when a quick action may be needed, even if it never occurs (de Freitas et al., 2007; Tillman and Ambike, 2018, 2020); and (2) a drop in the synergy index (anticipatory synergy adjustment, ASA, Olafsdottir et al., 2005) timed to the initiation of the quick, self-paced action. ASAs have been observed in young, healthy persons 200-400 ms prior to the time of action initiation (Kim et al., 2006; Zhou et al., 2013).
The analysis of stability in multi-element systems extends further to the perceptual domain. A considerable feature of perception is the capacity for perceptual invariance—i.e., the ability for some percept to remain stable in character over varying afferent and efferent components which comprise perception. For example, walking in a gallery is associated with the veridical percept of stable environment despite the fact that all modalities of relevant sensory information supply time-varying signals and the efferent processes also change continuously. The kinesthetic system is characterized by an abundant set of afferent and efferent elements contributing to perception; as such, it allows the CNS to create a space where a particular percept remains stable in spite of possible changes in the contributing signals. Such a subspace had been referred to as an Iso-Perceptual Manifold (IPM; Latash, 2018).
Consider the example of co-contraction of the agonist-antagonist muscles crossing the elbow, as in Figure 3. It is easy to co-contract the biceps and triceps muscle without changing the angle of the elbow in the process. For a majority of individuals, this task will result in nearly no motion of the elbow, which will be properly perceived, showing that the kinesthetic percept of elbow angle remained stable despite a variety of changes in all the afferent and efferent signals associated with co-contraction.
Figure 3
Effects of agonist-antagonist co-contraction. Elbow flexors are defined as positive torque producers and are labeled as agonists. A: The referent coordinate (RC) at the level of muscle group (equivalent to λ from Fig. 1) specifies its force-length characteristic. The resultant torque-angle characteristic defines the joint angle and torque (equal to 0 assuming no external load).
B: During co-contraction, a change in the C-command results in opposite shifts of agonist and antagonist force-length characteristics. Efferent and afferent activity to/from both agonist and antagonist musculature increase. The percept of joint position remains unchanged despite changes in all salient afferent and efferent signals.
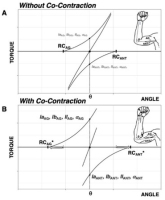
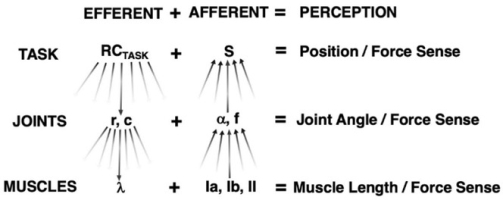
Figure 4
Kinesthetic Perception at Different Hierarchical Levels. RCTASK undergoes a sequence of few-to-many transformations to R- and C-commands at the joint level.
Each R- and C-command undergoes further few-to-many transformations to individual muscle λ. Sensory endings within muscles comprise many-to-few transformations to form joint angle/force information. Similar many-to-few transformations occur at the joint angle and force level to comprise information of endpoint position and force sense.
Problems with action stability in PD
A considerable body of evidence suggests that the neural control of action stability is impaired in PD (reviewed in Latash and Huang, 2015). Two aspects of synergic control show impairments at relatively early stages of PD: stability (as reflected in decreased synergy indices, ΔV) and agility (as reflected in shorter and smaller ASAs). In particular, Park and colleagues (Park et al., 2012) demonstrated significantly diminished synergy and ASA indices in a finger force production task performed by patients with Hoehn and Yahr stage-I and -II of PD. It is important to mention that stage-I is characterized by unilateral PD symptoms, but impaired synergic control was seen in both hands. Falaki et al. (2017) reported similar findings in studies of multi-muscle synergies in whole-body tasks performed while standing. Notably, the differences from age-matched controls were seen in stage-II PD, i.e., prior to the onset of clinically identified postural instability. Pre-clinical changes in movement stability (as measured by the synergy index) have been reported in a study of asymptomatic professional welders with known manganese accumulation in the basal ganglia (Lewis et al., 2016).
Indices of synergic control are sensitive to dopamine-replacement therapy, such as L-DOPA (Park et al., 2014, Falaki et al., 2017), whereas deep brain stimulation in PD improves indices of agility (longer and larger ASAs) but not indices of stability (Falaki et al., 2018).
Similar impairments in both aspects of the neural control of stability – stability and agility – are observed in patients with cerebellar disorders (Park et al., 2013). These observations support the idea of involvement of both major trans-cortical loops, via the basal ganglia and via the cerebellum, in ensuring action stability in line with the hypothesis of distributed processing modules introduced by Houk (2005). In contrast to the lesions of the basal ganglia and the cerebellum, patients with cortical stroke do not demonstrate changes in synergy indices in reaching and finger force-production tasks (Reisman and Scholz 2003; Jo et al., 2016).
Within a hierarchical system of efferent-afferent coupling for kinesthetic perception (Figure 4), these changes in action can be represented by changes at any level of the efferent components. It is possible that impaired action stability in PD is likely a consequence of impaired stabilization of the RC(t) at the task level. Synergies stabilizing task-level RC by co-varied adjustments of lower-level control variables have been reported in healthy persons (Ambike et al., 2016) but have not yet been studied in PD patients. Likely, these synergies are impaired in PD, which is expected to have implications for stability of perception. Indeed, if percepts are created by an interaction of task-level RC, RCTASK, with sensory signals (cf. Latash, 2018, 2019), loss of RCTASK stability is going to lead to estimation of the sensory signals in a wobbling reference frame resulting in unstable percepts (see later).
Changes in kinesthetic perception in PD
Despite its classification as a movement disorder, the first symptoms typically experienced by people with idiopathic PD are perceptual: a loss in olfactory acuity typically predates the onset of motor symptoms in PD patients by a number of years (Postuma et al., 2012). Changes in sensory function have been documented in multiple sensory modalities in PD, including visual (Weil et al., 2016), nociceptive (Blanchet and Brefel-Courbon, 2018), and chemoreceptive (Doty and Hawkes, 2019), among other deficits beyond the scope of the current review. These deficits extend to kinesthesia: studies of kinesthetic perception in PD reveal disease-elicited changes in the kinesthetic senses, i.e. the sense of endpoint position and the sense of force production. These senses are investigated using kinematic and force-production tasks, respectively.
Kinematic Tasks
The sense of endpoint position has been studied in reach-to-target conditions where visual feedback of performance is removed, thus forcing one to use the kinesthetic senses to complete the task. In such conditions, subjects with PD are less accurate, more variable, slower, less smooth, and hypometric as compared to controls (Adamovich et al., 2001; Flash et al., 1992; Klockgether et al., 1995; Klockgether and Dichgans, 1994), revealing a PD-related change in the performance of tasks relying exclusively on kinesthetic information. These deficits are likely to be exclusively kinesthetic in nature, given that they vanish in trials with visual feedback of the effector even in the absence of visual feedback of the target (Adamovich et al., 2001; Klockgether and Dichgans, 1994).
Further, the difference between active and passive motion acuity is altered in PD. Muscle activation is accompanied by co-activation of the gamma-system, which is expected to lead to increased accuracy of joint angle estimations in healthy subjects; however, this improvement in accuracy under active conditions is not seen in subjects with PD (Zia et al., 2002). One interpretation of these observations is that the reduced accuracy in PD is associated with low stability in the efferent component of perception (RCTASK). In this case, an improvement in the resolution of sensory signals due to the higher gamma-activity may be ineffective. Indeed, imagine for simplicity that joint position sense is the sum of two components, efferent and afferent, as shown in Figures 4 and 5. If one of them shows very large errors, improving precision of the other component is not going to have a significant effect. It is important to note that PD patients demonstrate decreased elbow position match accuracy as compared to controls in both active and passive conditions (Zia et al., 2000).
Figure 5
Effects of PD on Kinesthetic Perception. Accuracy of perception of coordinate x, estimated as the SDx over successive trials, is defined by variability of the central component, SDRC, and of the afferent contribution, SDAFF. The perceived coordinate is equal to RC + ƒ(AFF) and is estimated about a point with coordinates {x, F}. Parkinson’s Disease is expected to lead to SDRC >> SDAFF, thus leading to similar effects under small and large SDAFF.
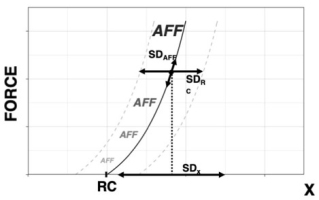
In purely passive conditions, patients with PD continue to demonstrate deficits in matching as compared to controls (Demirci et al., 1997). Maschke et al (2003) investigated sense of passive motion in subjects with PD, spinocerebellar atrophy (SCA), and healthy controls: subjects with PD demonstrated a significantly higher displacement detection threshold than SCA or healthy controls, as well as a higher percentage of indeterminate responses. Likewise, Konczak et al (2007) discovered that subjects with PD required larger limb displacements prior to detecting the presence of passive motion than healthy controls. Within a physical framework, sensory signals are always interpreted within a reference frame, even if its origin is under the level of muscle activation—i.e., the subject is relaxed and effector motion is produced passively. An interpretation within this framework is that the observed results could also be due to the reduced accuracy in RC at the effector level.
The nature of these PD-induced deficits in position sense have been further studied by utilizing muscle vibration. Muscle vibration is highly effective in stimulating velocity-sensitive primary spindle endings (Brown et al., 1967; Matthews and Stein, 1969). This increased firing often, but not always, produces a sensation of motion compatible with muscle lengthening; this illusion has been named the vibration-induced kinesthetic illusion (Goodwin et al., 1972; Lackner and Levine, 1979; Roll et al., 1989; Roll and Vedel, 1982). In targeted kinematic tasks, antagonist muscle vibration is expected to elicit undershooting (i.e., hypometria) due to an illusion of excess antagonist lengthening. Antagonist muscle vibration does elicit this expected hypometria in PD patients, although to a lesser degree than in controls (Rickards and Cody, 1997). Interestingly, a normal hypometric response to antagonist vibration can be elicited in the apparently unaffected limb in early-stage PD (Rickards and Cody, 1997), suggesting that the blunted response to antagonist vibration in patients covariates with basal ganglia pathology.
In summary, in kinematic tasks without vision, subjects with PD undershoot the target, move more slowly, and demonstrate more variability in limb trajectory and in task performance. The acuity of detection both passive and active motions is decreased; further, the expected kinematic response to antagonist muscle vibration is muted in subjects with PD.
Force Production Tasks
Muscle vibration induces not only kinematic illusions, but also illusions during force production in isometric conditions (Cafarelli and Kostka, 1981; Cuadra et al., 2021; Reschechtko et al., 2018). These results are expected from the scheme of control with RC (see Fig. 1A and 4) because a combination of RC and sensory signals defines an equilibrium point, i.e., a combination of coordinate and force. Patterns of vibration-induced force illusions suggest that vibration affects not only the sensory component of perceptions but also its efferent copy component, i.e., a copy of the RC command taking part in the perceptual process.
Vibration has been used to investigate the perception and production of force in isometric conditions in PD. Tan et al (2011) investigated the effects of patellar tendon vibration on targeted isometric force production into knee extension in healthy controls and PD patients with and without freezing of gait (FOG). The authors predicted that agonist muscle vibration would elicit an illusion of agonist muscle lengthening, and therefore, in contrast to the aforementioned studies, a compensatory increase in agonist force production would be seen. In a tertiary analysis of 30% MVC force trials in FOG patients, the authors observed target overshooting in the absence of vibration, and undershooting with vibration, even in the presence of visual feedback. No significant within-group differences were found by manipulating vibration or visual feedback in PD patients without FOG, or controls, suggesting that vibration-induced changes in force production may have a differential effect on PD patients with FOG over patients without FOG. In trials without vision of the target, vibration induced a small decrease in undershooting in PD-FOG subjects, in line with aforementioned findings, but this effect was small, non-significant and reversed in the non-FOG and control subjects. While this suggests impairments in sense of force in patients with PD, the effects of PD on sense of force production and the effects of agonist muscle vibration on kinesthetic perception in PD patients require further research.
Interpretation within the idea of RC control
Here we offer an interpretation of the reviewed findings in PD based on the introduced scheme of kinesthetic perception within the scheme of control with RC. Consider a kinesthetic task in PD, as illustrated in Figure 5. At the level of the single muscle, the relationship between efferent and afferent processes can be described symbolically as
where x is the perceived coordinate, RC the efferent process, and ƒ(AFF) the function of afference created within the central nervous system. Across trials, variability will be observed in both efferent component, RC, and afferent component, AFF, contributing to uncertainty in kinesthetic perception. The documented impairments in performance stabilizing synergies (reviewed in Latash and Huang 2015) predict relatively low stability in the task-related RC within the scheme in Figure 4. This translates into higher variability of RC and/or higher detection threshold during its changes. Assuming for simplicity a linear summation of the two components of kinesthetic perception:
If one of the summands in the right side of Eq. (2) is much larger than the other summand, e.g., if SD(RC) >> SD(AFF), kinesthetic errors are expected to be due primarily to the increased SD(RC). As a result, manipulations expected to affect SD(AFF), such as using muscle vibration or comparing active vs. passive movement, may be inefficient. We assume that in healthy persons, the two summands are about equal, SD(RC) ≈ SD(AFF), and, as a result, there are significant differences between conditions with manipulations of SD(AFF). These effects disappear in PD when SD(RC) dominates due to the impaired synergies in the efferent process. Note that this interpretation reduces problems with kinesthetic perception in PD to the documented problems in motor control.
Basal ganglia and synergies
As suggested in the earlier section on the changes in motor synergies in PD, the basal ganglia are highly important for stability of action. Other conditions associated with impaired function of the basal ganglia are well-known to demonstrate behavioral changes suggesting loss of stability in movements to varying degrees. In particular, Huntington’s disease (HD), a genetic disease causing degeneration of striatal projections to the globus pallidus and substantia nigra, is characterized by chorea: dance-like, writhing movements, representing an inherent loss in stability of movement (Ghosh and Tabrizi, 2018). Hemiballismus, a condition following injury to one of the subthalamic nuclei, is characterized by poorly-controlled, large-amplitude movements of the contralateral extremities. While no quantitative studies of synergies have been performed in patients with HD or hemiballismus, it is anticipated that such indices would confirm impaired synergies across motor tasks. The importance of the basal ganglia for synergic control is consistent with studies of asymptomatic welders who show changes in the synergy index during multi-finger force production tasks (Lewis et al., 2016).
The basal ganglia are important not only for motor function. Indeed, neuropsychiatric findings are nearly as ubiquitous as changes in movement stability in patients with basal ganglia disorders, and often predate motor symptoms by a number of years in HD and PD (Andres and Darbin, 2018). Primary diseases of the basal ganglia nearly unanimously affect cognition: both PD and HD are associated with neuropsychiatric phenomena, particularly in later-stage disease, with up to 90% of PD patients and 98% of HD patients demonstrating neuropsychiatric symptoms including changes in cognition (Obeso et al., 2014). Likewise, the most commonly reported psychomotor deficit in drug-naïve patients with psychiatric conditions is spontaneous parkinsonism, which includes the full repertoire of cardinal signs: tremor, rigidity, bradykinesia, and postural instability (Peralta et al., 2012). These clinical observations suggest that the basal ganglia may function to stabilize not only motor actions, but kinesthetic and cognitive functions as well.
Note that the idea of synergic control has been generalized recently to perception and, tentatively, to cognition (Latash, 2019). All these functions have common features such as the involvement of abundant sets of elements in typical tasks and stability of the outcome of an action with respect to its salient features in the presence of varying trajectories in the respective space of elemental variables. Examples from kinesthetic perception have been mentioned. In the field of cognition, finding an optimal move on the chessboard may result from different thought processes, expressing a thought with natural language may include different words, phrases, and prosody, etc. It is expected, therefore, that stability of the outcome of all those actions may suffer from injuries to brain structures, such as the basal ganglia, essential for the synergic control.
With respect to kinesthesia, stability of a percept requires that the naturally varying combinations of efferent and afferent variables do not leave the corresponding IPM (Latash 2018). This requirement cannot be easily split into two parts: stability of the efferent component, RCTASK, and stability of the afferent contribution. Nevertheless, stabilization of RCTASK by co-varying RC to elements (cf. Ambike et al. 2016) may be seen as beneficial for perceptual stability. The documented drop in indices of synergies in movement studies suggests that this factor, by itself, can contribute to problems with kinesthetic perception.
Other factors may include lack of the normal co-variation within the afferent set of signals as well as between the efferent and afferent sets. For example, the history-dependent function of muscle spindle activity (e.g., due to thixotropy, Proske and Gandevia, 2012) may cause difficulty in interpreting kinesthetic tasks which require varying changes in force levels and effector positions. Overall, changes in the interactions between efferent and afferent contributions to kinesthetic percepts in PD have barely been explored.
Conclusions
The capacity of biological systems to organize multi-element synergies to stabilize salient variables during both action and perception is a non-trivial feature of their physiological organization. Studies based on the principle of abundance and the UCM framework have provided ample evidence for action-stabilizing synergies and their impairments in patients with PD. The formal transition from efferent stability to perceptual stability is represented through the IPM concept, within which efferent and afferent signals together contribute to kinesthetic perception. So far, there have been only a handful of studies based on this concept limited to kinesthetic perception in healthy persons.
Impaired neural control of stability in PD suggests direct effects on kinesthetic perception that can account for some of the observations without invoking problems with the sensory component of perception. Clinical observations in other populations with basal ganglia injuries also support the basic idea that the basal ganglia play a crucial role in ensuring proper synergic control during various actions, motor, perceptual, and perhaps cognitive. While hypotheses on impaired synergic control of movements in PD have received experimental support, experiments designed to falsify hypotheses with respect to kinesthetic perception remain incomplete and are candidates for future lines of inquiry into stability of action and perception in PD.


