Physical Approach to Biological Movement

Biological movements obey laws of nature just like movements in the inanimate nature. Some of these laws are well-known, in particular the Newton Laws, and they can predict movements of inanimate objects if their initial states, parameters, and forces acting on them are known. This is not the case for biological objects. We have no evidence that they violate classical laws of nature, but their behavior is not dictated by these laws. In particular, they frequently walk or crawl uphill and swim against the current, which is very much atypical of inanimate objects. By themselves, these observations suggest that biological movement obeys other, currently unknown or poorly known, laws of nature. In this review, we assume that the goal of research in movement science is to discover such laws and their origins within the physiological structures; this assumption forms the foundation of the physical approach to biological movement (reviewed in Latash 2017, 2019).

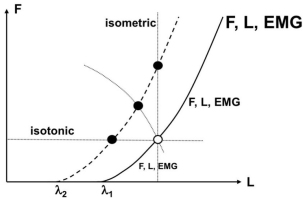
According to one of the approaches developed within the physical approach, the central nervous system (CNS) controls movements by setting time-varying magnitudes of spatial referent coordinates (RCs) for the effectors (reviewed in Feldman 2015). RC is the origin of a spatial frame of reference, which may also be viewed as a spatial attractor for the effector. This approach started with the introduction of the equilibrium-point hypothesis (Feldman 1966, 1986), which associated RC for a muscle with the threshold, λ, of its stretch reflex (Figure 1). Note that setting a value of λ does not prescribe peripheral variables typically measured in movement studies such as muscle activation, force, and length. All these variables also depend on the external force field. In particular, changing λ from λ₁ to λ₂ (Fig. 1) can produce a change in the muscle force (in isometric conditions), length (in isotonic conditions), or both (if the muscle acts against a coordinate-dependent force field). One may say that the behavior of an intact muscle is defined by a law of nature that links two salient variables, muscle force and length (for simplicity, we do not consider here derivatives of those variables), with the help of a single parameter, λ.

Figure 1

Neural control variable for a muscle is associated with its stretch reflex threshold (). Setting a value of defines a relation between muscle active force (F) and length (L); it does not define specific magnitudes of those variables (and of muscle activation level, EMG), which change along the F(L) characteristic. Shifting (from ₁ to ₂) shifts the F(L) characteristic and can lead to different peripheral consequences depending on the external load. Three loads are shown with dotted lines, and three new different muscle states are shown with filled circles.

In inanimate nature, changes in movement are produced by forces (variables within laws of nature), not of parameters that are commonly viewed as constants or changing relatively slowly. For example, in the Second Newton Law, F = m•a, force (F) and acceleration (a) are variables that are constrained by the law, and m is a parameter that is not constrained. This means that a change in force always leads to a change in acceleration, not in mass, although, mathematically, F = m•a or F = a•m are equivalent. Biological movements differ in a qualitative way from movements in inanimate nature: The CNS produces movements using parametric control, i.e., by changing λ without prescribing changes in mechanics. The idea of parametric control may be viewed as a development of an insight by Nikolai Bernstein (1947,1967) that the brain cannot in principle prescribe details of peripheral mechanics.

The general concept illustrated in Fig. 1 can be generalized for any effector up to the whole body. The CNS is assumed to specify time profiles of RC at the task level, the highest level in the neuromotor hierarchy, for example for the tip of the index finger during pointing movements. Further, a sequence of few-to-many transformations leads to the emergence of RCs at lower levels such as those of individual joints and muscles (and maybe even motor units). Such transformations are abundant (Gelfand and Latash 1998; Latash 2012). This means that a low-dimensional input defines a high-dimensional output in such a way that the variable controlled by the input remains stable despite possible variations in the output variables. For example, if a person is asked to repeat a multi-joint movement multiple times, the end-effector trajectory remains less variable and more stable as compared to the trajectories of individual joints (e.g., as in the classical study of blacksmiths by Bernstein 1930).

Recently, the principle of abundance has received support in many studies using the framework of the uncontrolled manifold (UCM) hypothesis (Scholz and Schöner 1999; reviewed in Latash et al. 2007; Latash and Zatsiorsky 2016). According to the UCM hypothesis, actions involving large (abundant) sets of variables produced by elements (elemental variables) are characterized by a specific structure of inter-trial variance reflecting stability of a task-specific salient performance variable. More variance is expected within the subspace where the salient variable does not change (the UCM for that variable) as compared to the orthogonal to the UCM subspace (ORT) where this variable changes. Of course, the inequality V_UCM > V_ORT is not guaranteed because the CNS is free to stabilize or not to stabilize a performance variable by co-varied adjustments of elemental variables. For example, if the purpose of an animal is to facilitate change, for example during preparation to a quick action or in the process of learning, controlled loss of stability may be beneficial (e.g., Olafsdottir et al. 2005; Kozyrev et al. 2018)

The UCM hypothesis offers a set of tools that allow asking the CNS questions: Do you care for (stabilize) such-and-such variable? Do you care about this variable more or less than about a different variable, or across different conditions, or across different populations? An index, ΔV, reflecting the normalized difference between V_UCM and V_ORT has been used as an index of a synergy stabilizing specific performance variables.

Physical Approach to Kinesthetic Perception

The physical approach has recently been developed for the field of kinesthetic perception (Latash 2018a). Note that links between action and perception have been studied for a long time (reviewed in Kugler and Turvey 1987; Turvey 2007) and, recently, have received support from neurophysiological studies of cortical mirror neurons that are active during both action observation and performance (reviewed in Rizzolati and Craighero 2004; Fadiga et al. 2005). One of the influential concepts in the field has been that of efferent copy (von Holst and Mittelstaedt 1950; see also the related concept of corollary discharge, Sperry 1950). According to the original concept, signals from alpha-motoneurons ("motor command") to a muscle participate in predicting changes in sensory signals from proprioceptors within the muscle. These changes, addressed as reafference, induce reflex changes in muscle activation and affect perception of muscle state only if they deviate from the prediction. In contrast, changes in sensory signals induced by external forces (exafference) always produce reflex effects and affect perception. This scheme has been criticized recently (Feldman 2015, 2016), in particular because it is unable to account for the ability of humans to relax following a voluntary movement. Nevertheless, the basic idea that efferent processes provide means for estimating signals from peripheral receptors and generating percepts has been developed within the idea of control with RCs.

Within the physical approach, setting a value of λ to a muscle is, by itself, solving part of the problem of perceiving muscle force and length. Indeed, prior to setting this value, any combination of force and length was possible (a two-dimensional array, see Fig. 1). After λ has been set, only force-length combinations that belong to the stretch reflex characteristic are possible, i.e., only points that belong to a one-dimensional array. Sensory signals from various sources may be used to locate a specific point on the force-length characteristic and lead to perception of both muscle force and length.

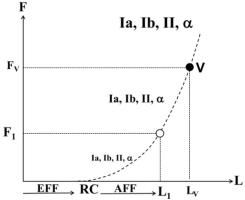
According to one of the simplified schemes (Feldman and Latash 1982; Feldman 2009), efferent (motor) processes define a referent point in spatial units (RC in muscle length units) and afferent (sensory) processes inform on the deviation of the actual state of the muscle from the RC (Figure 2). Note that the scheme in Fig. 2 suggests that artificial changes in sensory signals are expected to lead to parallel effects on perceived muscle length and force. This prediction has been confirmed in studies of the effects of high-frequency muscle vibration. Muscle vibration has been known for many years to induce illusions of joint position and velocity (Goodwin et al. 1972; Roll and Vedel 1982), sometimes even corresponding to anatomically impossible joint positions (Craske 1980). Traditionally, these illusions were interpreted as consequences of the unusually high frequency of firing of primary spindle afferents sensitive to muscle velocity and, as a result, highly sensitive to vibration. According to the scheme in Fig. 2, however, a change in sensory signals should lead to illusions of both muscle length and force (see point V). Such force illusions have been reported (Cafarelli and Kostka 1981; Reschechtko et al. 2018) in support of the scheme for combined perception of force and length.

Figure 2

Perception of muscle length and force gets contributions from efferent (EFF) processes and afferent (AFF) processes. EFF defines a referent point in spatial units (RC) and AFF informs on the deviation of the actual state of the muscle from the RC. Signals from various peripheral receptors and from α-motoneurons increase monotonically along the F(L) curve. Muscle vibration is expected to lead to illusions of both muscle length and force (F_V and L_V, see point V) different from the actual values F₁ and L₁.

The idea of afferent-efferent interactions during kinesthetic perception has been combined recently with the principle of abundance (Latash 2018a). Indeed, numerous sensory endings of many modalities contribute to perception of a relatively small number of salient mechanical variables. For example, perception of joint position and moment of force can get contributions from articular receptors, sensory endings in muscle spindles and Golgi tendon organs in all muscles crossing the joint. All these sensory endings are directly sensitive to local deformation, and the amount of deformation reflects joint position and/or moment magnitude. For example, when a person co-activates muscles acting about a joint without moving the joint, signals from all major peripheral receptors change due to changes in tendon force, joint capsule tension, muscle fiber length, and activation of gamma-motoneurons. Nevertheless, the joint is correctly perceived as motionless. This means that the changes in afferent and efferent signals during muscle co-activation are constrained to a manifold corresponding to stable perception of this low-dimensional variable – joint position. This manifold has been addressed as iso-perceptual manifold (IPM). Note that local sensitivity of sensory endings to mechanical variables may not be crucial for perception of salient, low-dimensional variables. This is demonstrated by observations of basically unchanged joint position sense after total joint replacement (Cross and McCloskey 1973; Grigg et al. 1973) and by a number of recent physiological studies (Watson et al. 1984; Luu et al. 2011; Proske and Gandevia 2012).

The principle of abundance seems to be truly universal. Indeed, most human actions, from single-finger pressing (involving multiple muscles and motor units, i.e. abundant at some levels of analysis) to cognitive actions, may be viewed as motion to a target defined in a corresponding multi-dimensional space of elements involved in the action. All such actions are characterized by the availability of numerous solutions and stability of salient variables across those solutions. For example, telling a story multiple times is typically associated with different words and phrases, while the gist of the story remains unchanged (Latash 2019).

Any new theoretical framework is only as good as its ability to offer new, logical and based on laws of nature, explanations for known phenomena and to predict new non-trivial phenomena i.e., draw predictions that cannot be drawn based on other frameworks. In the next few sections, we present several examples of such novel interpretations and novel behavioral phenomena, primarily from the field of finger force production but not limited to those tasks.

Unintentional Drifts in Performance

The first well-known phenomenon we would like to consider is the unintentional force drift during accurate force production tasks in the absence of visual feedback (Slifkin et al. 2001: Vaillancourt and Russell 2002). Accurate force production is highly sensitive to visual feedback (e.g., Reschechtko et al. 2014, 2017), and removing feedback typically leads to a gradual force drop by up to 40% or even more if the initial force level is not very low (e.g., over 15% of maximal voluntary contraction force); the time exponent of these force changes is within the range of 10-20 s (Ambike et al. 2015). For lower initial forces, the drift is smaller and it can reverse for very low forces, possibly due to adaptation of pressure sensitive cutaneous and subcutaneous receptors (e.g., Iggo and Muir 1969).

Initially, typical force drifts to lower magnitudes were described in terms of limitations of the working memory, and this explanation received indirect support from clinical and imaging studies (Vaillancourt et al. 2001, 2003; Poon et al. 2012). Later studies, however, cast doubt on this interpretation by showing that, when subjects are asked to match the actual force over the course of the force drift with the contralateral effector or with the same effector after a short break, they reproduce not the actual reduced force magnitude, but the initial force level and sometimes even overestimate it (Solnik et al. 2017; Reschechtko et al. 2018). So, the downward drift does not seem to be due to forgetting the initial force level and replacing this memory with a smaller force magnitude. We will offer a different explanation for the force drift, which is based on the idea of control with RCs and allows to generalize this explanation for other tasks and effectors.

Force production in isometric conditions by a single effector (e.g., a finger) along a coordinate X is associated with setting RC values for the agonist and antagonist muscle groups, RC_AG and RC_ANT (Fig. 3A). This results in a dependence of force on X, F(X), which is shown schematically as a straight line in Fig. 3 and can be described with two parameters, its intercept and slope, RC and k: F = –k•RC assuming that the actual effector coordinate is zero. Shifting both RC_AG and RC_ANT along X in the same direction shifts the F(X) characteristic, i.e. changes RC without a change in k. This type of control has been addressed as reciprocal command or R-command. Shifting RC_AG and RC_ANT in opposite directions rotates the F(X) characteristic, i.e. changes k without a change in RC. This type of control has been addressed as coactivation command or C-command (Feldman 1980, 1986, 2016). The presence of two commands at the control level makes this mechanically non-redundant task abundant at the control level. Three combinations of RC and k are illustrated in Fig. 3B, which are equally able to produce the same force at the same fingertip coordinate.

Figure 3

A: Force production in isometric conditions by an effector along a coordinate X is associated with setting RC values for the agonist and antagonist muscle groups, RC_AG and RC_ANT. This results in a dependence F(X) shown as a straight line defined by two parameters, intercept and slope, RC and k: F = –k•RC. The presence of two commands at the control level (R-commands defines RC; C-command is shown by the double-pointed arrow) allows to use multiple combination of RC and k to produce a target force level (three of those are illustrated in panel B). C: The idea of RC-back-coupling is expected to lead to a drift in both RC_AG and RC_ANT toward zero resulting in force drift toward lower magnitudes (from the open circle to the filled circle).

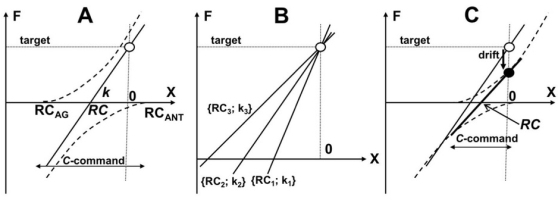
RCs play the role of attractors for the effectors. As a result, natural behavior of the system is expected to lead to a reduction in the distance between RC and the actual effector coordinate. In non-isometric conditions, this naturally leads to net force production that moves the effector toward RC. In isometric conditions, the effector cannot move and the only way to minimize the distance between RC and the actual effector coordinate is motion of the former toward the latter. Imagine that both RC_AG and RC_ANT start to move to coordinate zero in Fig. 3A. This can be expected to lead to a drift of RC toward zero and a drift of k toward lower magnitudes (see Fig. 3C). The hypothetical mechanism of RC drift has been addressed as RC-back-coupling; it fits naturally a few schemes on the control of multi-element natural actions (Latash et al. 2005; Martin et al. 2009).

Indeed, both RC and k drifts have been reported in experiments with fingertip force production (Ambike et al. 2016; Reschechtko and Latash 2018). In those studies, RC and k were measured using smooth, brief positional perturbations applied to the fingertip (with the “inverse piano” device, Martin et al. 2011, illustrated later in Fig. 8) and measuring the force changes under the instruction to the subject “not to interfere voluntarily with force changes”. A similar drift in k toward lower values was also observed when the subjects had visual feedback over the whole time of the trial, i.e., in the absence of force drift (Reschechtko and Latash 2018). In those conditions, RC was adjusted by the subjects to keep force constant. These observations suggest that the drift in k, produced by a drop in the C-command leading to lower coactivation within agonist-antagonist pairs, is a widespread phenomenon.

Figure 4

A schematic illustration of a task with two effectors producing a fixed magnitude of their summed outputs: E₁ + E₂ = const. The solutions space (UCM) for the task is shown with the slanted solid line. The orthogonal to the UCM space (ORT) is shown with the dashed line. Stabilizing (E₁ + E₂) is expected to lead to an elliptical trial-to-trial data point distribution shown with the gray ellipse. Processes within the UCM are expected to show lower stability and lower speed (the potential field is shown as φ_UCM), while processes within ORT are expected to show high stability and high speed (the potential field is shown as φ_ORT).

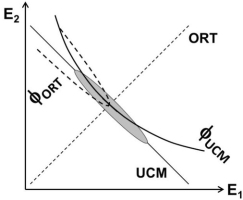
Figure 5

The task to produce a certain level of force (open circle) is associated with a pair of values of the referent coordinate and apparent stiffness, {RC₁; k₁} that define a force-coordinate characteristic (solid line, open circle). Increasing the C-command without a change in the R-command is expected to lead to force increase due to an increase in the apparent stiffness, k (dashed line, {RC₁; k₂}, black circle). To decrease the force deviation, an increase in the C-command has to be coupled to an adjustment in the R-command (a shift of RC toward smaller absolute values, dotted line, {RC₂; k₂}, gray circle).

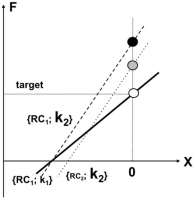
Figure 6

During force-matching tasks, subjects do not match both referent coordinate and apparent stiffness, RC and k, but co-adjust these two parameters to ensure that they fit the same hyperbolic UCM. Typically, the match hand shows smaller k values and larger absolute RC values.

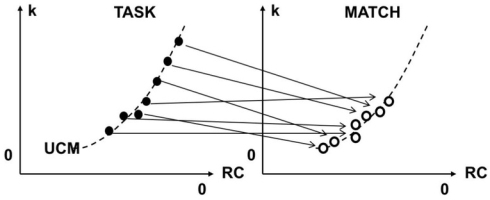
Figure 7

Two elements contribute to a jointly produced variable. The vertical coordinate, E, reflects the efferent process (which involves more than one variable!), and the two other axes reflect afferent signals from the two elements (A₁ and A₂, each of them is also multi-dimensional!). The gray triangle (IPM – iso-perceptual manifold) illustrated schematically the subspace where perception of the commonly produced variable is stable.

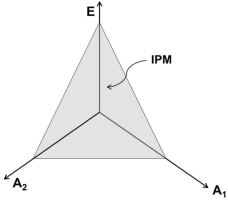
Figure 8

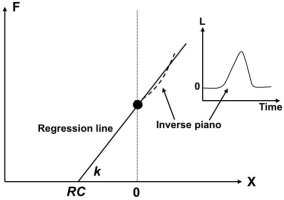
If a person produces a certain level of force in isometric conditions at a certain, initial coordinate of the effector (X = 0), transient lifting of the effector (insert) leads to unintentional force change (the dashed line). In a linear approximation, the regression line, F(X) may be used to compute RC (intercept) and k (slope).

Note that an unintentional drift in a performance variable is a sign of lost stability of that variable. Several studies estimated stability of total force produced by a set of fingers within the framework of the UCM hypothesis in different spaces, those of finger forces, hypothetical commands to fingers (finger modes, Danion et al. 2003) and also in the {RC; k} space (Reschehtko et al. 2014; Parsa et al. 2016, 2017; Reschechtko and Latash 2018). All the mentioned studies have confirmed a drop in the indices of stability, for example those reflecting the normalized difference between the amount of variance within the UCM and within ORT, ΔV = (V_UCM – V_ORT)/V_TOT where V_TOT stands for total variance and all indices are computed per dimension in the corresponding spaces.

The idea that performance drifts can be produced by unintentional drifts of RC toward the actual effector coordinate leads to predictions of similar drifts in other tasks. Of course, if available sensory signals are sufficient to provide the subject with information on the actual value of a salient variable, no drifts in this variable are expected because of feedback-based corrections of performance. The force drift experiments suggest that the natural perception of force is rather poor and, as a result, subjects are unaware of rather large force changes, up to 40% of the original magnitude. Even larger drifts were documented for moment of force produced by a set of fingers in pronation-supination (Parsa et al. 2017; Reschechtko and Latash 2018). These drifts were commonly over 50% of the initial moment magnitude, and some subjects even showed reversals of the moment direction (from supination initial moment to pronation moment), which they were unaware of.

When a salient performance variable is perceived accurately by the subject, it is not expected to show unintentional drifts and observing the hypothetical effects of RC-back-coupling requires some trickery. In particular, no predicted drifts are observed in tasks that require keeping a certain posture in space, from arm posture to whole-body posture. However, asking a person to perform a cyclical task centered about a certain value of a salient variable allows observing drifts in whole-body tasks (Rasouli et al. 2017). Applying a transient force perturbation with a dwell time between the perturbation application and removal to the hand involved in a hand positioning task also leads to drifts in the hand position (Zhou et al. 2014, 2015). Such perturbation-induced drifts are much faster as compared to the spontaneous force drifts; the faster drifts show exponent times of 1-2 s.

The presence of performance drifts at two, rather different, time scales, 1-2 s vs. 10-20 s, suggests that these processes originate in different spaces. Note that processes within the UCM for a performance variable are expected to be slow corresponding to relatively low stability within the UCM. In contrast, processes within the more stable space, ORT, are expected to be fast. This is illustrated in Fig. 4 using a cartoon task of two-effector total force production. The Figure shows presumed potential fields along the UCM and along ORT, which correspond to low stability and slow processes in the former, and high stability and fast processes in the latter. Steady-state tasks are expected to be associated primarily with processes within the UCM, i.e. to be slow. Tasks with purposeful changes in a variable (such as cyclical force production, Ambike et al. 2016b) and those with external perturbations (Wilhelm et al. 2013; Zhou et al. 2014) are associated with large deviations of the system in ORT and, therefore, with faster processes.

Motor and Perceptual Effects of Muscle Co-Activation

Co-activation of agonist-antagonist muscle groups is a very common phenomenon observed across tasks and populations (reviewed in Smith 1981; Latash 2018b). If one views the purpose of muscle activation as the generation of desired net force and moment vectors, co-activation is obviously wasteful because activation of an antagonist muscle requires energy and reduces the net force. Co-activation has been traditionally viewed at the level of joint, limb, and whole-body mechanics as the means of increasing apparent stiffness (cf. Latash and Zatsiorsky 1993) of the effector, which is expected to contribute to its ability to produce fast movements (by increasing the natural frequency) and to resist external perturbations. The latter assumption is not trivial because increasing apparent stiffness contributes to stability of a kinematic chain with a fixed origin, but not kinematic chains with free origins, such as the human body during standing. Indeed, a few recent studies have provided evidence that stability of the human vertical posture is reduced by co-activation of major postural muscle groups (Yamagata et al. 2019, 2020).

An alternative explanation for the function of co-activation has been proposed (Latash 2018b). According to this explanation, the role of co-activation is to ensure abundance at the level of control variables, such as the R-command and C-command, which is crucial for stabilization of performance at the level of control by co-varied adjustments of these two basic commands. In particular, when a person performs a motor task in precarious conditions, e.g., during standing on a narrow or slippery surface, co-activation increases to provide a safety zone, where co-varied adjustments of the R- and C-commands can be used, in spite of the mentioned negative effects of co-activation on postural stability. Neurological patients and other populations with reduced postural stability perceive everyday tasks as challenging and, therefore, typically show increased levels of muscle co-activation (Arias et al. 2012; Boudreau and Falla 2014; Hammond et al. 1988; Hirai et al. 2015; Keshner et al. 1987; Mari et al. 2014; Rinaldi et al. 2017).

The scheme of control with R- and C-commands leads to a number of non-trivial predictions with respect to possible motor and perceptual effects of muscle co-activation. Imagine that a person is asked to produce a constant force level by pressing with an effector (e.g., a finger) against a force sensor and then to increase co-activation of the hand and arm muscles without changing the level of pressing force (Fig. 5). Visual feedback on the force level is removed at the command to co-activate muscles. According to the illustration in Fig. 5, changing the C-command without a change in the R-command is expected to lead to force increase due to an increase in the apparent stiffness, k (compare the open and black circles). To decrease the force deviation, an increase in the C-command has to be coupled to an adjustment in the R-command (a shift of RC toward the effector coordinate in Fig. 5, the gray circle).

An experiment has shown that, indeed, subjects show a significant, large increase in force during co-activation (by about 50% of the initial force level), and then the amount of excess force drifts to lower values (Cuadra et al. 2020). The latter phenomenon is expected from RC-back-coupling, which was introduced in the previous section as the hypothetical mechanism for unintentional force drifts in conditions without visual feedback. Surprisingly, subjects were not only unaware of the force increase but they reported verbally that the force magnitude had actually dropped somewhat during the co-activation. To make the picture even more confusing, when the subjects were asked to match the pressing force with the contralateral homologous effector, they showed the increased force level with a tendency to overshoot it (Cuadra et al. 2020).

To interpret the results related to force perception, we have to consider the role of the two basic commands (R and C) and afferent information in two senses, sense of force and sense of effort. While force is a basic mechanical variable, effort is not. Sense of effort has been viewed as a primarily central phenomenon with relatively minor effects from afferent signals (McCloskey et al. 1974; Proske and Gandevia 2012). A number of studies have shown discrepancies between sense of force and sense of effort (Jones 1995; Monjo et al. 2018; Proske and Allen 2019). In particular, a series of studies by van Doren (1995, 1998) explored behavior of subjects who were asked to match forces applied by the index finger and the thumb to a cylinder held between these two digits. The cylinder could have various springs inside. As a result, to match forces, the subjects had to compress the cylinder differently depending on the stiffness of the spring. These studies have suggested that the subjects matched not forces but RCs, i.e. intrinsic variables better suited to be associated with sense of effort.

The results of the mentioned co-activation study suggest that the verbal reports by the subjects were related to their sense of effort, not force. As a result, the subjects reported not the force level but the magnitude of RC, which has already started drifting toward the actual effector coordinate, i.e., RC started to drop in its absolute magnitude (note that, within the system of coordinates in Fig. 5, RC is negative).

Force matching is a more complex action. The subject not only has to estimate the level of force by the instructed effector but then actually has to produce it with the contralateral effector. Note that a fixed force level by an effector, e.g., by a fingertip, corresponds to a UCM, i.e., a subspace in the abundant control space: The same force level can be produced with various {RC; k} combinations as illustrated in Fig. 3B and has been shown in several studies with accurate force production (Ambike et al. 2016a; Reschechtko and Latash 2018). So, to match force, the subjects had to either match both RC and k accurately, or to co-adjust these two parameters to ensure that they fit the same hyperbolic UCM (as illustrated in Fig. 6). A recent series of studies have shown that the subjects use the latter strategy: The natural variation in RC and k across repetitive trials showed only modest correlations with these two variables during force matching by the other hand (Abolins, Cuadra, Ricotta, and Latash, unpublished). This means that, to match forces, the subjects could not rely on sense of effort but had to actually attend to force magnitudes resulting in relatively accurate force matching.

Perception of Elements and of the Total

Imagine that you are asked to report, verbally or with a matching procedure, a mechanical variable, which is produced by coordinated changes in several body-related variables. Examples are reporting total force produced by a set of fingers during pressing, fingertip position during multi-joint movement, etc. This is easy to try. Press with the four fingers naturally on a rigid surface and then try to match either the total force with the other hand positioned symmetrically with respect to the trunk, or the force of one of the fingers. The former task feels much more natural and easy. Why? There are undistorted signals, both efferent and afferent, available for each of the fingers. However, focusing on one of the involved elements feels effortful and unnatural.

The IPM concept offers an explanation for the described phenomena. Indeed, consider Fig. 7. This figure uses only three dimensions (it is impossible to draw anything higher-dimensional on a piece of paper) to reflect perception of a variable produced by two elements, e.g., total force produced by two fingers. The vertical coordinate, E, reflects the efferent process (which involves more than one variable!), and the two other axes reflect afferent signals from the two fingers (A₁ and A₂, each of them is also multidimensional). Note that all the points within the IPM (the gray triangle – a very much simplified illustration!) correspond to accurate perception of the same total force magnitude. Different points within the IPM, however, correspond to perception of different forces by the individual fingers. This is partly due to the fact that the same total force can be produced by different finger forces (see the earlier Fig. 4 illustrating the UCM for this task) and partly – to the fact that the same force percept can correspond to different contributions from the efferent and afferent processes (see the earlier illustration in Fig. 2). To summarize, percepts of finger forces can vary without variation of the total force percept.

This prediction was explored experimentally using the force-matching method (Cuadra and Latash 2019). The study has shown that both variable and constant errors during finger force matching were significantly smaller when the finger acted alone as compared to conditions when it had to produce about the same force while being part of a multi-finger force production task. In a follow-up study (Cuadra et al. in press), both force matching and verbal reports were used. The force-matching method confirmed the results from the first study. The verbal reports, however, failed to show significant differences under the one-element and two-element conditions.

Earlier, we mentioned another example of a disparity between verbal reports and force matching during force changes induced by purposeful muscle co-activation (Cuadra et al. 2020). As suggested in the previous section, verbal reports could be dominated by the efferent component of the task, i.e. matching effort (RC) rather than force. This effectively reduces dimensionality of the space where stable percepts emerge, which could be the reason for the difference between the results of force-matching and verbal reports in one-finger and multi-finger tasks.

A number of studies provided evidence for more accurate matching of variables defined in external space, such as positions and orientations of body parts, compared to variables defined using body-related coordinates, such as joint angles (Soechting 1982; Worringham et al. 1987; Gooey et al. 2000). These observations are compatible with the IPM concept. Note that proprioceptors may be seen as providing signals more directly related to body coordinates rather than to the external world. The mentioned findings suggest that more accurate (and stable) percepts emerge at the level where signals from proprioceptors have to be combined with efferent signals, i.e. at the IPM level.

Perception of Force Changes Induced by Changes in External Force Field

Until now, we have discussed unintentional force changes (and drifts in other performance variable) that emerge spontaneously and may be seen as reflections of natural behavior of the effectors. More commonly, unintentional changes in performance variables are produced by changes in the external force field. Indeed, specifying values of control variables, such as RCs at different levels of the neuromotor hierarchy is only one of the factors defining motor performance. The other factor is external force field. For example, the same shift in the command to a muscle (λ) can produce force change (e.g., in isometric conditions), movement (e.g., in isotonic conditions), or both (see earlier, Fig. 1).

If a person produces a certain level of force in isometric conditions at a certain, initial coordinate of the effector (e.g., fingertip), lifting or lowering the effector is expected to lead to unintentional force change. If such a positional perturbation is applied smoothly and does not lead to jerky, poorly-controlled reflex and reflex-like reactions, and the subject in this mental experiment does not change the control variables (RC values), the force-coordinate time profile is expected to follow the F(X) line specified by the control signals. This is illustrated in Fig. 8. In linear approximation, the regression line, F(X) may be used to compute RC (intercept) and k (slope). This method has been used in many of the aforementioned studies to estimate RC and k values during finger force production with the help of a special device called “inverse piano” (Martin et al. 2011).

Does the subject perceive such unintentional changes in force adequately? Note that these changes supposedly take place without changes in the efferent commands, i.e. they are not expected to be associated with changes in sense of effort. A number of earlier studies have reported that subjects consistently overestimate forces applied to the body passively, by external devices (Sittig et al. 1987; Shergill et al. 2003, 2005). A recent study explored force matching during unintentional finger force changes induced by the “inverse piano” (Abolins et al. 2020). In contrast to the mentioned studies, there was a trend toward underestimating the actual force changes, and the errors were significant. There were consistent differences, however, in the magnitudes of the RC and k values used by the matching hand: About the same force magnitudes in the two hands were produced by the matching hand using significantly lower values of k and significantly larger absolute values of RC as compared to those values in the task hand. In other words, relatively accurate force matching was achieved by using values in the {RC; k} space that belonged to the same (or nearly the same) UCM but were shifted consistently along that UCM “down”, toward lower k values.

What could be the reason for these consistent differences between the hands? First, we have to make a disclaimer that these differences were seen not only during force matching during unintentional force changes but also during intentional force changes by the task hand of about the same magnitude. So, they reflect more global differences between two effectors during force matching. One reason why the task hand works with higher k values may be related to the earlier hypothesis that higher C-command (translated into higher k) affords a larger safety margin to ensure stable production of force. Indeed, the task hand had to produce accurate force levels over relatively long time intervals with possible force changes, intentional and unintentional. In contrast, the match hand only was required to produce relatively brief force-matching episodes without any surprises. This remains a very much speculative interpretation.

Concluding Comments

The described framework has shown its ability to offer novel interpretations for a range of well-known phenomena including unintentional drifts in performance, vibration-induced kinesthetic illusions, and the phenomenon of muscle co-activation. It has also led to the discovery of novel phenomena that naturally fit the framework and could hardly be predicted based on alternative views on motor control. This groups includes, in particular, the unintentional (and unreported!) large increase in force during muscle co-activation, vibration-induced force illusions, and high variability in matching the contribution of individual elements in multi-element tasks. Researchers should be encouraged to explore the richness of this approach and apply it to various subfields of movement studies including studies of athletics, movement disorders, and movement rehabilitation.