How might humans learn to use muscles?
Current theories and strategies for sensorimotor control reflect the historical confluence of three very different methodologies: psychology, physiology and engineering. Psychology provides the taxonomy of behavior – collecting observations and organizing them according to perceived patterns and statistical correlations. Physiology is a reductionistic approach to discovering the mechanisms that give rise to the psychophysical observations. Engineering is the invention of solutions to what are often similar problems that arise in the world of machines. Engineers sometimes take inspiration from mechanisms of nature and sometimes propose that their own inventions might provide insights into biological systems.
Theories of biological sensorimotor control and strategies for engineered sensorimotor control can both be divided into four general schemas:
Biological organisms and bespoke machines are subject to very different constraints that determine the relative suitability of the control strategies in Table 1. Both simple organisms and simple machines may be able to use preprogrammed Central Pattern Generators (CPGs) effectively to perform a limited and predictable set of tasks. This confers the advantage of achieving the required performance immediately out of the box or egg or womb. The vestiges of such solutions may be found in CPGs for breathing (Von Euler, 1983), hatching (Suster & Bate, 2002) and quadrupedal locomotion (M. Shik, Orlovskiĭ, & Severin, 1966; M. L. Shik & Orlovsky, 1976).
Table 1
All possible sensorimotor control schemes for organisms and machines fall into one or a combination of four strategies discussed in the rest of the text.
For more sophisticated systems and open-ended task sets, it may be necessary to learn solutions, but these take time to acquire and refine. Human infants make millions of trial-and-error movements before they are proficient enough to function (Piek, 2006), movements that would frustrate the purchasers of a robot and wear it out before it became useful. Engineers have devised efficient methods to shorten somewhat this period of “system identification” of the plant to be controlled and to embed the resulting information in mathematical models that permit online analytical solutions to achieve optimal control of any goal (Johansson, Robertsson, Nilsson, & Verhaegen, 2000).
For the most complex physical plants with many degrees of freedom and especially those with nonlinear properties such as biological musculoskeletal systems, analytical algorithmic solutions may not now (or ever) be computationally tractable or even theoretically feasible. One strategy is to simplify the plant by adding assumptions about the function of low-level circuitry that intermediates between commands and plant. Muscle synergies have been proposed as a mechanism that might reduce the number of degrees of freedom that the central command generator need consider to perform tasks. Servocontrol by proprioceptive feedback has been proposed as a mechanism to linearize the mechanical output of individual muscles in response to neural activation.
When it is not possible or advisable to simplify the plant sufficiently to enable analytical solutions, engineers increasingly turn to deep-learning neural networks, whose workings are inspired by at least some of the mechanisms that biological neurons employ to process, store and retrieve information. Neural network methodology has been applied widely and successfully to understand biological perception and to enable machine perception. Neural networks are particularly attractive for biology because they should be able to adapt rapidly and safely to a plant with highly complex, unpredictable and changing properties. These are conditions of both ontogenetic development and phylogenetic evolution. This review considers whether motor action might share the same cortical computational substrate as learned perception.
The topics below consider i) the complexity of the musculoskeletal system, ii) proposals to simplify this system in order to facilitate various control strategies, and iii) options to handle complexity that account for the motor behavior observed by psychologists and that might be embodied using biological components described by physiologists.
I have chosen to illuminate these topics with quotations from the work of Nikolas Bernstein (1896-1966), published originally in Russian starting in the 1930s and discovered by Western scientists after its translation in 1967. The quotes are identified here with the dates of the original Russian and German journal articles plus the page number from the currently accessible version (Whiting, 1984), which includes Whiting’s 1967 translation (Bernstein, 1967) plus invited commentaries from other researchers written in 1983. Unfortunately, most current researchers have not read these in any language and rely instead on the interpretations of those who claim the work as precedent and justification for theories that Bernstein had already considered and rejected. I confess to having been in that camp until recently and to being now both chastened and encouraged.
Is the musculoskeletal system redundant or overcomplete?
Bernstein’s original and oft-cited observation of redundancy came from painstaking inverse dynamic analysis of cinematographical records of natural human behaviors. Bernstein appears to have been the first to perform such rigorous analyses. It is a disservice to reduce them to such a trivial observation. Most tasks can be accomplished by different combinations of joint trajectories (kinematics) or muscle activations (kinetics) because the description of the task is inevitably under-specified. If a task is described simply as repositioning a fingertip from one key to an adjacent one while standing at a keyboard, then this kinematic task could be accomplished by repositioning almost any or all joints from the metacarpophalangeal to the feet. All of those movements are possible but we usually choose to type with metacarpophalangeal and perhaps some wrist movement because they are better suited to achieving speed and accuracy. An expert can type at 120 words/minute, which corresponds to 600 characters/minute or 10 characters/second. If the brain is confused by a plethora of redundant options, it isn’t confused for long.
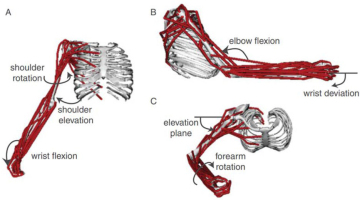
The kinetic redundancy that was of more interest to Bernstein and his many followers focuses on how the nervous system decides which muscles to use to create a particular kinematic trajectory (Figure 1). Again the problem is obvious. A child asked to “make a muscle” first activates the muscles to hold the forearm in a vertical posture with the shoulder abducted and then cocontracts the biceps and triceps brachii to bulge the muscles without changing the arm posture. If the task were posed only as “hold your forearm vertical with your shoulder abducted,” EMG data will show one pattern of muscle use; “make a muscle” produces a different pattern for the same kinematics.
Figure 1
Computer graphic of the human arm and forearm in the OpenSim platform for modeling musculoskeletal dynamics, consisting of 7 degrees of freedom (DOFs) and 50 simulated muscles; from (Saul et al., 2015) with permission of the publishers.
None of this apparent redundancy surprised or discomfited Bernstein, nor did it by itself suggest a solution:
“Knowledge about the processes of co-ordination is not obtained deductively from knowledge of the effector process.” N. Bernstein, 1940, p.233
Bernstein considered the solution of restrictions on available strategies and rejected it:
“Eliminating the redundant degrees of freedom…is employed only as the most primitive and inconvenient method, and then only at the beginning of the mastery of the motor skill, being later displaced by more flexible, expedient and economic methods of overcoming this redundancy through the organization of the process as a whole.” N. Bernstein, 1957, p.375
One solution to the redundancy problem is to recognize that motor tasks include explicit or implicit requirements and constraints beyond the description of the primary goal of the task (G. E. Loeb, 2000). The subject is often instructed to make movements at one or two joints while not moving others in order to standardize performance and facilitate analysis. Figure 1 shows 50 muscles operating 7 DOFs, but many of those muscles are multiarticular and act also on the numerous joints of the hand and fingers (distally) and cervical and thoracic vertebrae (proximally). Those joints were assumed to be rigid (called boundary conditions by engineers) in order to enable the forward simulation and inverse dynamic calculations that happened to be of interest to the authors. The total number of muscles in the hands, arms, shoulder girdle and cervicothoracic spine is not far from the mathematical minimum of two antagonist muscles required for each degree of freedom in the joints (G. E. Loeb, 2000).
In many motor psychophysical experiments, the subject may be considering the likelihood of internal noise or external perturbations, which would favor some of the otherwise redundant solutions over others (Francisco J Valero-Cuevas, 2016). The engineering concept of impedance provides a richer specification of a motor task that can be used to differentiate solutions that are redundant both kinematically (joint angles) and kinetically (net joint torques) until perturbed (Hogan, 1984a, 1984b). Impedance is a generalized way to describe the reactive forces that arise if a system is perturbed. It adds three dimensions to the kinematic specification of any task: stiffness (response to change of position), viscosity (response to change of velocity), and inertia (response to change of acceleration). Some of the stiffness and viscosity is the result of neurally mediated reflexes but a significant component reflects the intrinsic properties of muscles, which include highly nonlinear relationships between the length and velocity of the sarcomeres and the force produced at a constant level of activation (G.A. Tsianos & Loeb, 2017). By selecting different postural configurations for the same end-point, it is also possible to change the inertial response seen at the end-point (which is why it is wise to keep your elbow flexed when using your hand to feel for obstacles in the dark). By judiciously selecting different patterns of muscle coactivation that achieve the same net torques at the joints, the subject can enable useful “preflexes” that will generate forces that oppose perturbations without incurring the delays inherent in neurally mediated reflexes (Brown & Loeb, 2000). Similar strategies can reduce the effects of internal noise on the variability of forces exerted on objects (L. P. Selen, Franklin, & Wolpert, 2009; L. P. J. Selen, Beek, & van Dieen, 2005).
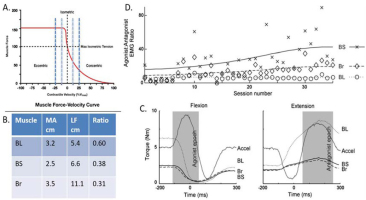
Muscles that are anatomical synergists may have important differences in their architecture that give them advantages or disadvantages for tasks with different kinematics. Many psychophysical tasks require large numbers of repetitions. If the subject understands this, then minimizing effort and avoiding fatigue constitute another implicit requirement of the task that would differentiate otherwise redundant solutions. Figure 2 illustrates the very slow and sometimes halting differentiation of three otherwise synergistic muscles into a new synergy pattern that achieves such a goal. The final patterns of muscle recruitment took advantage of architectural differences that affect their economy of force generation (energy consumed to produce a force-time impulse) for concentric vs. eccentric work.
Figure 2
A rhesus macaque was trained to perform a simple task requiring rapid and precise alternating flexion/extension movements of the elbow while the other joints were restrained. The task requires essentially the same joint torque to accelerate and decelerate the forearm but generating the same muscle force during the concentric (accelerating or agonist) phase requires higher recruitment and much higher energy consumption than during the eccentric (decelerating or antagonist) phase (G. A. Tsianos, Rustin, & Loeb, 2012). A. Force-velocity curve for sarcomeres. B. Three muscles – biceps long head (BL), biceps short head (BS) and brachioradialis (Br) – are synergists that are recruited together to generate flexion torque at the elbow but they have somewhat different musculoskeletal architecture. The ratio between moment arm (MA) and fascicle length (LF) governs the velocity seen at the sarcomeres for a given angular velocity at the elbow (dashed vertical lines in A.). C. Maximal force generating ability compared to isometric for each muscle during the typical acceleration profiles of the flexion and extension phases of the task. D. The animal performed several hundred such movements in each daily session (x-axis); the ratio of the integrated EMG amplitude during the agonist vs. antagonist phase (y-axis), which will always be substantially greater than 1 to compensate for the force-velocity relationship. For the first week, the ratios of each muscle were similar but they gradually diverged as the animal learned to use BS and Br preferentially to generate torque during the agonist phase. Data from (Cheng & Loeb, 2008).
Humans often use their limbs to generate forces on objects rather than to produce unloaded postures. The neural circuitry for such tasks has been less studied because of poor animal models and methodological complexity. Valero-Cuevas introduced the notion of “feasible activation space” for the 7 muscles that enable the human index finger to generate 3D force vectors at the tip (Cohn, Szedlák, Gärtner, & Valero-Cuevas, 2018; Francisco J Valero-Cuevas, 2016; Francisco J Valero-Cuevas, Zajac, & Burgar, 1998). Many patterns of muscle recruitment can generate a given low-force vector, but these apparently redundant solutions disappear gradually and naturally as the required forces increase. What remains is a family of patterns that change abruptly as the direction of this maximal force generation changes, suggesting that the nervous system is able to control these muscles independently when necessary.
Do muscle synergies reduce the dimensionality of motor control?
Synergies are extracted from multimuscle EMG records by any of several statistical methods for blind-source separation according to matrix factorization (Ebied, Kinney-Lang, Spyrou, & Escudero, 2018). What does that jargon mean in plain English? It means that the investigator already believes that the available EMG records do not span the space of all possible combinations but instead might be reduced to some unknown number of recurring and intermixed patterns. The question is then how many such underlying patterns are required to account for the data. That depends on how much data are available and what is meant by “account for.”
The importance of the data available for the synergy extraction can be appreciated by asking how many DOFs and synergies are present in a piano. We already know that the piano has 88 independently operable keys (DOFs), but a synergy analysis based on the performance of one musical composition would find that a much smaller number of recurring patterns could describe the ways in which the keys are played. If the analysis includes another composition in another key and genre, the number of recurring patterns (i.e. synergies) will be greatly expanded.
The criteria for claiming that a certain number of synergies account for the data are arbitrary, as is generally the case for statistics and probability. Extracting additional synergies is always possible and generally will then account for more of the underlying variance in the data, at least until the residual variance has been reduced to white noise. Many researchers assert that their synergies account for their data after they account for 90% of the variance (≥0.9 VAF). Nevertheless, the residual variance is usually considerably higher than the physical noise of the recordings, so why stop?
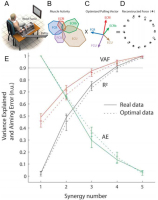
One way to consider whether residual variance may be relevant to the brain’s control of the musculoskeletal system is to ask what motor error might be introduced if that variance were uncontrolled. This turns out to be considerably higher as a result of the nonlinearities of the processes that convert electrical excitation (EMG) into myofilament activation, force production, torque generation and skeletal motion. For human locomotion, a forward simulation of trajectory from extracted synergies resulted in unacceptable errors that required considerable fine-tuning of the synergies to correct, defeating the purpose of synergies (Neptune, Clark, & Kautz, 2009). A similar forward simulation analysis for the simpler task of isometric force generation by 5 wrist muscles (Figure 3) shows that the criterion of variance accounted for (VAF) approaches values generally seen as acceptable (90%) with only 3 synergies, but aiming error would then be over 30%. Aiming error doesn’t decline to less than 10% until the number of synergies equals the number of muscles (Aymar de Rugy et al., 2013). A similar conclusion was reached for a virtual force task involving 10 shoulder and elbow muscles moving a splinted forearm (Barradas, Kutch, Kawase, Koike, & Schweighofer, 2020).
Figure 3
A. Subject generating isometric wrist forces in 16 directions. B. Patterns of activity of each wrist muscle (extensor carpi radialis longus, ECRl and brevis, ECRb; extensor carpi ulnaris, ECU; flexor carpi ulnaris, FCU; flexor carpi radialis, FCR) graphed radially for each direction. C. Pulling direction of each muscle. D. Validation of optimal control model to account for human performance while minimizing sum of squared muscle activations. E. Ability of number of synergies extracted to account for variance in the EMG records (VAF), the statistical correlation coefficient (R2) and aiming error (AE). Adapted from (Aymar de Rugy, Loeb, & Carroll, 2013) with permission of the publisher.
How many data points go into a synergy extraction depends on the number of EMG channels available as well as the number and variety of behavioral tasks recorded (Ebied et al., 2018). It is rarely feasible to record from all muscles that contribute forces to a set of tasks. The selection is usually determined by anatomical limitations on the placement of skin-surface EMG electrodes. That methodology often excludes or under-samples the deep, slow-twitch muscles that dominate low-force tasks (Chanaud, Pratt, & Loeb, 1991). EMG signals allegedly from deep muscles may be contaminated with cross-talk from superficial muscles, introducing spurious correlations (G. E. Loeb & Gans, 1986).
One way to test the utility of synergy extraction without such methodological limitations is to apply it to a synthetic data set with a completely known set of muscle activations that produce ideal performance and then see how well performance would be captured by the synergies instead of the optimal recruitment. This enables simulation of typical experiments in which EMG signals are available from only a subset of the muscles that contribute to the behavior. For the simple, 2D isometric forearm task illustrated in Figure 4, the ability of synergies to account for performance depended on which 8 of the 13 contributing muscles provided the EMG signals. Note that only 3 synergies account for ~90% of the EMG variance for both the feasible (redundant) and the ideal (less-redundant) subset, but the aiming error remains unacceptable (>30%, Fig. 5E) even after extracting 8 synergies for the 8 muscles that are most accessible experimentally but more redundant mechanically (Aymar de Rugy et al., 2013).
Figure 4
Isometric force vectors for 2D forearm (flexion/extension & pronation/supination) produced by 13 optimally recruited muscles (Supinator, SUP; the short and long heads of Biceps Brachii, BIC sh and ln; Brachialis, BRS; Brachioradialis, BRD; Pronator Teres, PT; Pronator Quadratus, PQ; the long, medial, and lateral heads of Triceps, TRI ln, m, and lt; Extensor Carpi Radialis longus and brevis, ECRl and ECRb; flexor carpi radialis, FCR). A. Pulling directions in 2D space for the 8 muscles typically recordable with surface EMG electrodes. B. Force vectors (red + symbols) toward 16 targets computed according to 1-8 synergies extracted (using multiple initializations) from the 8 somewhat redundant muscles recordable with surface EMG electrodes. C and D. Pulling directions for the 8 less-redundant muscles that better reflect the 2D task and simulated force vectors for synergies extracted for those muscles. E and F. Synergy performance as in Fig. 3. From (Aymar de Rugy et al., 2013) with permission of the publishers.
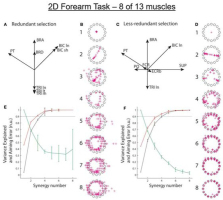
Figure 5
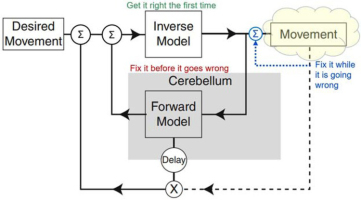
Simplified engineering block diagram for analytical control based on internal models of the system being controlled. The Forward Model predicts how the musculoskeletal mechanics of the plant will generate Movement in response to commands generated by the Inverse Model. If those commands include errors, the predicted movement can be compared to the Desired Movement to request corrective movements. The Inverse Model allows the controller to compute commands that will cause the Desired Movement (including corrective movements) to be produced by the plant. Dashed lines indicate sensory feedback, which is substantially delayed by musculoskeletal mechanics and neural conduction velocity. Adapted from Manto et al., 2013.
What neural mechanisms are responsible for motor behavior?
Chasing Metaphors
The strategies discussed below in more detail have often been presented in somewhat ambiguous language that might be summarized as follows:
Human subjects exhibit limited patterns of muscle recruitment as if they had access only to a limited set of synergies.
Human subjects perform tasks as if they were computing optimal patterns of muscle use from internal models of their musculoskeletal system.
Physiologists are interested in such statements to the extent that they describe mechanisms that lead to experimentally testable hypotheses. Does “as if” connote mechanism or metaphor? If only metaphor, then the observations that they claim can be restated in much more prosaic form:
While worth noting, statements i and ii are rather mundane observations rather than testable hypotheses; they have little value for reductionist science. The discussion below considers the mechanisms implied by statements 1 and 2 as well as alternative mechanisms that would account for observations i and ii.
It is useful to consider the historical context that led to interest in mechanisms 1 and 2 above, which are not mutually exclusive. In one of the commentary chapters in the 1984 reprint, Bernstein was chided for discarding the possibility of an analytical solution for the “more flexible, expedient and economic methods of overcoming this redundancy through the organization of the process as a whole”. Geoffrey Hinton pointed to a recently developed, simplified Newton-Euler solution for inverse dynamics that had been implemented as software for a PDP11 minicomputer (Luh, Walker, & Paul, 1980) to argue that an internal model of the musculoskeletal plant might be used by the nervous system as part of the computation of motor output (Hinton, 1984). Hinton further proposed “synergies” to eliminate the remaining redundancy to decide which muscles to use to generate the required torques at each joint, despite Bernstein’s rejection of that simplification and the above-noted problem of multiarticular muscles.
Internal Models to Compute Motor Output
For musculoskeletal systems and behaviors that are too complex for genetically preprogrammed solutions, the nervous system might compute analytical solutions to motor control problems as they occur; for overviews see (Shadmehr & Krakauer, 2008; Wolpert, Miall, & Kawato, 1998). The general form of engineered analytical solutions includes both a forward and inverse model that describe the behavior of the musculoskeletal plant (yellow cloud in Fig. 5). This idea has been fully developed and substantially validated as a representation of the oculomotor system for control of eye movements (Girard & Berthoz, 2005; Manto et al., 2013). It is often assumed to generalize to limb control. The eye is a very special motor plant, however. It is a single ball-and-socket joint with negligible inertia and friction that is controlled by 6 muscles arranged in 3 pairs of antagonists that act orthogonally on its 3 DOFs. The oculomotor pools receive little or no proprioceptive or cutaneous feedback; adaptive control is based on visual slip of the image on the retina, which is tightly coupled to the eye movements produced by the muscles. These unique simplifications make it feasible for the cerebellum to construct and calibrate forward and inverse models through neurophysiologically realistic learning (Kawato, 1999; Kawato & Gomi, 1992).
Feasibility of Internal Models of Limbs
None of the oculomotor simplifications are relevant to the musculoskeletal system of the rest of the body. In fact, they don’t even explain visual gaze, which often includes ballistic movement of the head as well as the eyes (Vliegen, Van Grootel, & Van Opstal, 2005), using the highly complex musculoskeletal linkage of the cervical spine (Richmond, Singh, & Corneil, 2001). In addition to mechanical complexity (Fig. 1), limb motor pools receive massive amounts of sensory feedback. Engineers often use such feedback for a local servocontroller that linearizes the behavior of each motor, simplifying the inverse model required by the controller in order to compute the feedforward commands. Does such feedback in biological systems (blue dotted line in Fig. 5) provide a similar simplifying assumption for the brain?
In principle, the excitatory feedback from the muscle spindle stretch receptors could be used when desired to stabilize the length of individual muscles or the position of a joint if such servocontrol loops were configured reciprocally in antagonist pairs of muscles. The inhibitory feedback from the Golgi tendon organs could be used to stabilize the force output of individual muscles. A combination of the two servocontrols could be used to stabilize stiffness, the ratio of force to length, and a component of impedance control (Houk, 1979). Such feedback circuits had been identified by Sherrington in the cat spinal cord. Similar feedback circuits were in widespread use for the servocontrol of the motors used in many physiological experiments. The servocontrol metaphor gave rise to “Merton’s hypothesis” (Marsden, Merton, & Morton, 1976; Merton, 1953), “equilibrium point control” (Asatryan & Feldman, 1965; Bizzi, Hogan, MussaIvaldi, & Giszter, 1993; Feldman & Levin, 1995), “motor partitioning” (Windhorst, 1979; Windhorst, Hamm, & Stuart, 1989), “stiffness control” (Houk, 1979), and “task groups” (G. E. Loeb, 1985). All of these have fallen out of fashion as the interneuronal connectivity of the spinal cord was probed further (see subset illustrated in Figure 6). It became clear that these circuits reflected a much broader control scheme (Eccles & Lundberg, 1958; Jankowska, 2013; Jankowska & McCrea, 1983; Pierrot-Deseilligny & Burke, 2005). Furthermore, much of the descending control from the brain converges on this interneuronal circuitry (Eccles & Lundberg, 1959; Rathelot & Strick, 2009) rather than the originally proposed final common pathway of the motoneurons (Sherrington, 1906). From the brain’s perspective, the yellow cloud in Figure 5 must be extended to include this convergent circuitry (oversimplified for illustration as the blue summing junction) as well as the musculoskeletal apparatus (discussed further below).
Figure 6
For skeletal linkages with more than one DOF (e.g. 2 DOF planar elbow-shoulder schematic at upper right), many muscles work sometimes as synergists and sometimes as antagonists (i.e. Partial Synergists). The afferent and interneuronal connectivity among their alpha motor pools (α) includes Modeled Pathways that subserve both relationships. Descending control from the brain synapses mostly on these interneurons and presynaptically on their individual inputs to facilitate or inhibit transmission and on two types of gamma motoneurons that determine the length and velocity sensitivity of the spindle Ia receptors in each muscle (Raphael, Tsianos, & Loeb, 2010). For the 6 muscle model system, this results in 438 variables that the brain adjusts to prepare for a movement (SET) and a subset that command the movement itself (GO) (George A Tsianos, Goodner, & Loeb, 2014). Note that this model omits the extensive feedback from cutaneous receptors via oligosynaptic interneuronal circuits, which have not been well-characterized.
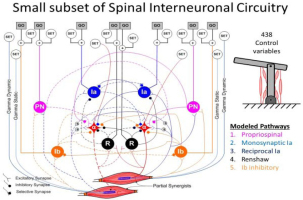
Yet another engineering tool has been applied in order to understand the spinal circuitry as a programmable regulator – a multi-input, multi-output form of servocontrol whose matrix of gains can be reset dynamically to achieve desirable states (He, Levine, & Loeb, 1991; G. E. Loeb, Levine, & He, 1990). Engineering tools such as linear quadratic regulator (LQR) design (Athans & Falb, 1966) and optimal feedback control (Koppel, Shih, & Coughanowr, 1968) were originally devised to provide analytical solutions for complex industrial systems like refineries and rockets. Computing the optimal biological solutions requires a metric for the cost to be minimized (see below) plus an invertible model of the musculoskeletal system, which is difficult but feasible with some simplifications. The solutions include the net gains from each sensor to each actuator rather than the details of interneuronal circuitry, but the gains correspond to the most prominent spinal interneuron types (modeled in Figure 6). They suggest a plausible substrate for the convergence of descending control and proprioceptive feedback (G. E. Loeb et al., 1990).
Experimental Evidence for Internal Models
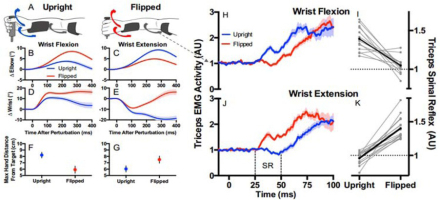
Direct evidence of active programming of a regulator can be seen in the ability of the brain to reverse the shortest latency, heteronymous stretch reflexes from the wrist muscles to the elbow muscles in order to facilitate stabilization of the hand position when the wrist is in a pronated vs. supinated posture (Figure 7) (Weiler et al., 2019). It is fair to say that the spinal cord functions as if it were a regulator programmed by the brain, but this begs the question of how that program is computed. The algebraic algorithms used by engineers to compute optimal regulator gains have no known analogs in neural circuitry, nor is there any mathematical method to apportion them among the diversely connected interneurons of the spinal cord.
Figure 7
Subjects were asked to maintain the position of a handle against a steady load requiring elbow extension by the triceps brachii muscles from which EMG was recorded. A-G. Sudden force pulses perturbed the handle randomly in either direction with the forearm and wrist in the upright (pronated; blue traces) or flipped (supinated, red traces) posture. H-I. Perturbations that flexed the wrist and stretched the wrist extensor muscles resulted in heteronymous short latency reflexes (25-50ms, limited to spinal circuits) that excited the triceps in the upright position (which would assist with recovering the target position) and inhibited it in the flipped position (which would prevent it from opposing the recovery). J-K. Perturbations that extended the wrist also generated spinal reflexes that were reversed appropriately for the task. From (Weiler, Gribble, & Pruszynski, 2019) with permission of the publishers.
The shortest latency reflexes are interesting to neurophysiologists because they can be attributed unambiguously to spinal circuitry, but they are only a small component of the complete response to perturbations. The larger, longer latency responses (such as those seen after 50ms in Figure 7) provide enough time for any pathway to contribute up to and including sensorimotor cortex, where timely neural activity corresponding to the perturbation and the response has been recorded (MacKinnon, Verrier, & Tatton, 2000). Optimal feedback control has been developed as a theory of computation for the motor cortex and voluntary behavior in general (Liu & Todorov, 2007; Pruszynski & Scott, 2012; Scott, 2004; Todorov & Jordan, 2002). By carefully designing the cost function, the performance achieved by such optimal controllers can be altered to better match experimental data. Cost functions typically require some admixture of terms related to level of effort (e.g. muscle activation, forces produced, energy expended, etc.) and to accuracy of performance (e.g. trajectory following, end-point error, variance as a result of noise, etc.). Unsurprisingly, cost functions that emphasize end-point accuracy in the face of noise or perturbations often account well for experimental data when such accuracy is the explicit instruction to the subject. It is useful to understand the nature of the mechanical problems thereby solved but optimal feedback control does not provide hypothetical mechanisms for how they are solved. If optimal feedback control is a description of performance rather than a theory of mechanism, then it comes down to saying that the nervous system is good at finding solutions that are close to optimal for the goals of a task (G.E. Loeb, 2012).
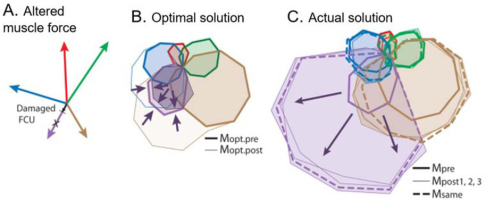
If motor programs are computed as needed from internal models, then performance should improve steadily toward optimal as the internal model is refined through practice. If the musculoskeletal plant changes, there must be a mechanism to update its internal model. Muscles can change their force generating capabilities in the long term in response to exercise patterns and in the short term in response to fatigue or injury. Figure 8 shows an example in which subjects accommodated to a short-term change in one muscle simply by increasing the same pattern of recruitment rather than making adjustments consistent with a revised internal model (A. de Rugy et al., 2012). This result is equally consistent with fundamentally limited synergies as well as motor habits that persisted over 1.5-2h and 750-800 trials in this experiment. The synergies that are extracted from the behavior may eventually change (as in Fig. 2) as the subject learns to deal with a chronic change (Nazarpour, Barnard, & Jackson, 2012). In that case, new synergies would then suggest motor habits that can be learned and adapted rather than reflecting hardwired simplifications of redundant musculature. It is worth noting that belief in the malleability of motor habits provides the conceptual basis and the tools for the professions of physical therapy and athletic coaching.
Figure 8
A. Subjects performing the 2D isometric wrist force task described in Fig. 3 were exposed to active lengthening of one tetanically stimulated wrist muscle (flexor carpi ulneris, FCU), which produced a short-lived reduction in force generation of 15-73%. B. Optimal recruitment patterns for the 16 target directions before and after accounting for this reduction. C. Actual recruitment patterns before and after the reduction. From (A. de Rugy, Loeb, & Carroll, 2012), with permission of the publishers.
The addition of intermediary circuitry between command and motor output plus the integration of sensory feedback in that intermediary circuitry result in two important effects on the motor control problem. First, this essentially precludes the development of an internal model of the plant, much less an inversion of this model by which to compute optimal command signals. If the brain had internal models of the plant that it was trying to control, those models would have to include all spinal interneurons and their connectivity to the motor pools and each other as well as the mechanical dynamics of the musculoskeletal system itself (i.e. everything in Fig. 6 extended to all muscles in the body). Second, descending control of these interneurons greatly expands the redundancy problem (discussed further below) because multiple combinations of command signals to the interneuronal circuitry can result in the same nominal behavior of the plant (George A Tsianos et al., 2014).
“The motor effect of a central impulse cannot be decided at the centre but is decided entirely at the periphery….The decisive role in the achievement of motor control must be played by afferentation and that it is this which determined the physiological conductivity of the peripheral synapses and which guides the brain centres in terms of the mechanical and physiological conditions of the motor apparatus.” N. Bernstein, 1940, p.235.
Learned Repertoire
If it is impossible to generate the forward and inverse models of the plant that are required by the strategy depicted in Figure 5, then solutions must be learned and recalled rather than computed online.
“The process of practice towards the achievement of new motor habits essentially consists in the gradual success of a search for optimal motor solutions to the appropriate problems….Practice…does not consist in repeating the means of solution to a motor problem time after time, but in the process of solving this problem again and again by techniques which we changed and perfected from repetition to repetition.” N. Bernstein, 1957, p. 382.
The feasibility of a “search for optimal motor solutions” instead of computing them from models depends on what is meant by success. If the number of elements to be controlled by the brain includes all the various interneuronal circuits as well as the motor pools, then the dimensionality of the problem is vast. Neither an analytical solution nor an exhaustive search is feasible, so finding optimal as the one best strategy to minimize a cost function is simply not possible (G.E. Loeb, 2012). Instead, higher organisms that learn tend to improve their mean performance over time. Such a strategy of gradual optimization is unlikely to discover the globally optimal solution and it is likely to get stuck in motor habits that are suboptimal (what engineers call a local minimum in the cost function). It is usually important, however, for an organism to discover good-enough solutions quickly. The acceptability of this strategy depends on the density of and ease of finding good-enough solutions afforded by the very high-dimensional and highly redundant set of circuits that are controlled by the brain.
The schema illustrated in Figure 9 was implemented for control of 2 DOF musculoskeletal models for the wrist and for a coplanar elbow and shoulder (Raphael et al., 2010; George A Tsianos et al., 2014; G. A. Tsianos, Raphael, & Loeb, 2011). The spinal-like regulator for planar arm movement consisted of 6 muscles (2 antagonist pairs of monoarticular muscles and 2 biarticular muscles), each equipped with realistic models of spindle primary (Ia) afferents under fusimotor control (γdynamic and γstatic) and Golgi tendon organs (Ib) and with connectivity subject to presynaptic inhibition/facilitation (see circuitry outlined in Fig. 6). Distributed interneuronal circuits included the classical connectivity for Ia monosynaptic excitation of synergists and reciprocal inhibition of antagonists, widespread Ib inhibition, Renshaw inhibitory feedback from motoneuron collaterals, and propriospinal convergence of Ia and Ib excitation with the learned commands en route to motoneurons. This resulted in 438 separate, initially randomized gains (all receiving premovement SET values and a subset receiving movement initiating GO values) that the controller had to learn to adjust in order to accomplish center-out reaches (Fig. 10A). For simplicity, the GO commands were simple step functions that contained no information about the phases of the movement or the temporally modulated recruitment of muscles required to accelerate, decelerate and stabilize the distal limb on the target (Fig. 10B). Nevertheless, it was always possible to arrive at good-enough sets of gains that produced dynamic muscle activation patterns (Fig. 10B), kinematic behaviors and energy consumption similar to those observed experimentally.
Figure 9
Engineering block diagram for good-enough control in which cerebral cortex performs trial-and-error learning and storage of motor programs that control the state of lower sensorimotor centers such as the spinal cord, where they are integrated with sensory feedback from the musculoskeletal system. The tasks to be performed are indexed, recalled and evaluated in sensory coordinates (Gerald E Loeb & Fishel, 2014; Scott & Loeb, 1993), which facilitates computation of cost as difference between sensory feedback expected and received. Reprinted from (G.E. Loeb, 2012) with permission of the publishers.
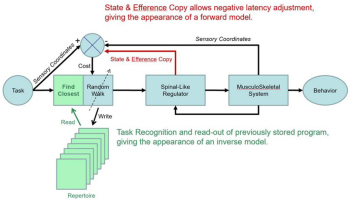
Figure 10
Performance of the learned repertoire control shown in Figure 9. A. Model system for center-out reaching task with 6 muscles (colored lines) operating coplanar hinge joints at elbow and shoulder to perform center-out reaching tasks to blue targets (4 of 16 illustrated). B. Reach trajectories (open circles = 10ms steps) and muscle activations (colored lines) after training to targets T1 and T2 and interpolating to generate reach to Ti. Incremental training consisted of starting with randomized spinal circuitry control variables, learning to reach T1 and then modifying the same program to learn to reach to T2; Reinitialized indicates re-randomizing starting condition before learning to reach to T2, for which interpolation is unreliable. C. and D. Ability of incremental training to generate learned programs that interpolate for both distance to the target and speed of the reach. Adapted from (George A Tsianos et al., 2014), which includes additional examples of learning and interpolation of movement programs that cope with complex external loads called curl-fields (perturbing force orthogonal and proportional to velocity in desired direction of reach).
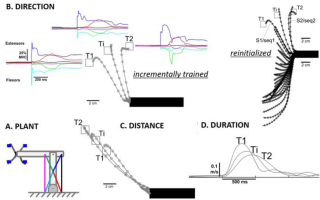
Importantly, the solution gain sets for different initializations of the model system depicted in Figure 6 tended to be very different (George A Tsianos et al., 2014). Rather than rerandomizing the gains to learn each new task, starting with one good-enough solution and modifying it incrementally to perform other tasks resulted in sets of solutions that could be easily interpolated to achieve performance goals that were intermediate between those for which fully trained solutions were available (Figure 10B-D). Such a strategy results in families of muscle recruitment that might be described efficiently by statistical extraction of synergies, but no such synergies existed in the system before training.
Good-Enough Programs vs. Optimal Control of Synergies
Elements to be Combined
The storage of motor programs rather than their on-line computation from internal models raises the question of how many programs must be stored to support the very wide range of tasks that humans learn to perform (G. E. Loeb, 1983). This would be greatly reduced if a relatively coarse repertoire of programs can be interpolated to perform tasks with intermediate parameters such as direction, distance and speed (as illustrated in Fig. 10) and even complex loads (e.g. learning and interpolation of viscous curl fields demonstrated by Tsianos et al., 2014). In that sense, the learned, good-enough strategy shares something with synergies, which must also be weighted and combined to generate any behavior. The difference is that an individual “good-enough” program is good enough to generate one useful behavior, whereas an individual synergy is not. It is immediately obvious how an infant performing thousands of trial-and-error movements might learn, store and recall good-enough programs that generated useful movements. Interestingly, roboticists are starting to consider strategies whereby robots can explore complex environments, learn iteratively to perform tasks and build upon a repertoire of solutions to address ever more complex tasks (Forestier, Mollard, & Oudeyer, 2017). By contrast, no mechanism has been proposed to learn synergies from scratch; they must be extracted statistically from observations of mature behavior.
The proponents of synergies generally assume that the observed synergies are embodied by neural circuits that are hard-wired rather than learned, sometimes referred to as primitives (Giszter, 1992). Some stereotypical circuits that might be genetically preprogrammed constitute the CPGs for the most primitive and innate behaviors such as the coordination of quadrupedal locomotion. Quadrupedal locomotion in the cat is under the control of a spinal CPG that can generate such stereotypical patterns of motoneuron activity even in the absence of sensory feedback (M. L. Shik & Orlovsky, 1976). Nevertheless, idiosyncratic differences exist in muscle activation and reflex response patterns in intact, normally behaving animals (G. E. Loeb, 1993). Asymmetries can be induced by unilateral surgical alteration of hindlimb musculoskeletal mechanics at an early age (G. E. Loeb, 1999). Furthermore, there is little reason to expect the elements of quadrupedal locomotion to provide a useful basis for playing soccer or eating with utensils. It seems unlikely that primitives enabling such learned skills arose in phylogeny or ontogeny before the skills themselves, skills that human infants require years to acquire.
Good-enough control requires another type of primitives – a set of spinal circuits that mix descending commands with sensory feedback and project onto various combinations of motor pools. There is no question that such circuits exist. The analytical tool used to identify optimal reflex gains to stabilize standing posture in the cat generated patterns that bore a striking resemblance to the most prominent circuits that have been identified by neurophysiologists, suggesting that these circuits are well-designed primitives (G. E. Loeb et al., 1990).
It is unclear which details of the apparently well-designed spinal and other lower sensorimotor centers are hard-wired genetically and which might arise from Hebbian self-organization during spontaneous motor activity in the fetus (D'elia, Pighetti, Moccia, & Santangelo, 2001; Kiehn & Tresch, 2002) and motor babbling in the infant (Caligiore et al., 2008; Lee, 2011). Many of these centers are also under the direct and indirect control of the cerebellum, which has its own learning algorithms (Koziol et al., 2014). A judicious combination of genetically specified and learned control of basic connectivity would provide the sort of malleable substrate required to accommodate the evolution of new species (Enander et al., 2019). Such evolution is driven by random mutations of the musculoskeletal and other hardware that enable improved performance of some important task, but such a mutation will not persist unless the first individual in which it occurs can immediately take advantage of it (Partridge, 1982). If the spinal circuitry primitives that form in an individual animal in some way reflect the musculoskeletal mechanics of that individual, this challenge becomes tractable. Such adaptive circuit primitives then might enable efficient trial-and-error discovery of sets of motor commands from the brain to these circuits that could take full advantage of both normal and mutated musculoskeletal mechanics.
Storage and Recall of Good-Enough Programs
The schema presented in Figure 9 proposes that tasks be defined in the brain by the complete set of sensory feedback that is expected when the task is being performed successfully. Sensory is defined broadly to include all sensory modalities (somatosensory, visual, auditory, etc.) plus efference copy signals regarding the state of the plant while performing the task. The various areas of the neocortex consist of neural networks that would function as an associative memory that stores a repertoire of previously learned tasks, indexed according to this sensory information and associated with the descending programs that performed them.
In order to perform a task, the brain must first associate the sensory information that calls for the task (e.g. the appearance of a desirable target object) with this stored sensory representation of the task being successfully performed (e.g. object acquired). That representation is then associated with the stored motor program that last performed the task. More than one such program may be recalled if the parameters of the task lie between those of the nearest stored programs. The weighted sum of those associated motor programs constitutes the motor output to the Spinal-Like Regulator, which integrates it with concurrent sensory feedback and sends it to the motoneurons and musculoskeletal system. Before, during and after the movement, state and sensory feedback to the brain can be compared to the sensory coordinates of the task to generate a Cost (a plausible function of cerebellum). If the discrepancy is unacceptable, the program can be tweaked by the Random Walk generator and tried again. The functions of judging acceptability and recruiting cortex to attend to shortcomings seem compatible with a value computation that has been proposed for basal ganglia, which is then transmitted to cortex via the thalamocortical pathway (Bosch-Bouju, Hyland, & Parr-Brownlie, 2013; Nakajima & Halassa, 2017). If the tweaked program is better than the previously stored program, it can be stored in its stead in the cortical Repertoire. Because the gains being tweaked randomly (via cortical output to the Spinal-Like Regulator) have no simple relationship to improvements or deteriorations of performances, such repeated practice appears to an observer as a random-walk.
Storage of tasks in sensory coordinates and their association with outputs in motor coordinates (descending commands to the Spinal-Like Regulator and other sensorimotor structures as described below) provide an opportunity to unify and integrate the classically separate behavioral activities of perception and action (Gerald E Loeb & Fishel, 2014). Complex perceptual tasks such as visual scene recognition or haptic object identification are generally performed iteratively as a sequence of motor actions that shift gaze or move fingers, in turn motivated by judgments about the degree of concordance with previous experience. Familiar scenes and objects are recognized according to the sensory information so obtained, which must be integrated contextually with the exploratory actions that led to that information (Subramanian, Alers, & Sommer, 2019). The internal representations of previously experienced entities in a self-organizing neural network are gradually refined with repeated exposure. Once an entity is recognized, the brain often needs to recall and consider what actions (motor commands) and outcomes (sensory signals) have been associated with the entity in order to make strategic plans. The schema in Figure 9 might then apply to virtually all cortical areas, which have broadly similar cytoarchitecture and plastic connectivity consisting of ascending afferent information, descending efferent projections and reciprocal projections with other cortical areas (Diamond, 1979).
Responses to Perturbations and Errors
Most of the literature on synergies is based on the study of unperturbed motor tasks. Compensations for errors and perturbations greatly increases the dimensionality of the problem (F.J. Valero-Cuevas, Venkadesan, & Todorov, 2009). Accounting for behavior then requires the addition of yet more synergies, which defeats the simplifying purpose for which they were proposed in the first place (Soechting & Lacquaniti, 1989). This problem can be overcome by allowing synergies to be combined not just by adjusting their weights but also by adjusting their temporal phases (d'Avella, Fernandez, Portone, & Lacquaniti, 2008; Safavynia & Ting, 2012). This little addition adds a lot of complexity to the putative neural controller of any such synergies. It also provides the experimenter with twice as many free variables with which to account statistically for behavioral data sets. Furthermore, the synergies required to account for perturbations must be added to the synergies that account for the unperturbed behavior. As described above, the addition of more behaviors and more perturbations of those behaviors and a tightening of the VAF (variance accounted for) all lead inexorably to the need to extract yet more synergies. It is unlikely that the final tally will be less than the reductio ad absurdum suggested by allowing both amplitude and phase to be controllable: if each synergy consisted of the recruitment of one muscle, then the number of synergies required to account perfectly for any and all possible EMG patterns must be equal to the number of muscles.
For good-enough control, the motor programs that are looked up and interpolated are sensorimotor programs that automatically set the gains of the circuits responsible for the reflex responses because they are the same circuits that generate the nominal, unperturbed behavior (Fig. 6). Descending commands are often described as generating excitation of motor pools that happens to be modulated by ongoing sensory feedback, but the same commands can also be interpreted as enabling selected reflex responses to that sensory feedback. In order to learn commands that anticipate perturbations requiring appropriate reflexes (as seen in Fig. 7), the trial-and-error learning of those motor programs must include a representative set of the perturbations that might occur. The huge increase in redundancy presented by the numbers of command parameters required to control the spinal interneurons offers many good-enough solutions for the nominal task but fewer that also enable good-enough handling of those perturbations. Nevertheless, if good-enough solutions can be found readily, it does not matter that optimal feedback control solutions can neither be found nor computed. Given the inevitable noise and variability of biological data, it may not even be possible to distinguish good-enough from optimal. This presents a problem for experimental falsification of either theory by psychophysical data.
Noise, Variability and the Learning Curve
The psychophysical data already contain information that appears to falsify model-based control. All model-based optimal control strategies discussed above imply that what is learned are changes and improvements to the internal model(s) that must be stored in the brain, rather than the motor programs that are thereby computed analytically. That, in turn, implies that motor performance should improve gradually as the model is refined and that residual variability of an over-learned task should reflect simple, stochastic, computational noise. Neither appears to be true.
Data from experiments that require learning a new skill are usually summarized in learning curves that show gradual improvements in performance. Those learning curves are usually constructed from averaged performance during long training sessions or running averages over many trials. This obscures the much larger trial-to-trial variability that is better described as a random walk (Gallistel, Fairhurst, & Balsam, 2004) and which is familiar to anyone trying to acquire a new skill. During acquisition or optimization of difficult skills, even running averages from day to day may show large deviations from steady improvement (e.g. Fig. 2).
Importantly, a random walk through a local cost function does not look like simple noise because the next output depends on the cost analysis of the previous output (the Read-Write loop in Fig. 9). The fluctuations in force generated during a simple, isometric force task have been attributed to “motor noise” in the stochastic firing patterns of motor units (Jones, Hamilton, & Wolpert, 2002). These fluctuations generally demonstrate constant variance (standard deviation as a percentage of mean force) but a careful examination of the force variability in the frequency domain reveals features incompatible with motor noise (Slifkin & Newell, 1999). Furthermore, detailed models of motor unit recruitment and force generation reveal that constant variance would not result from the physiology of motor unit recruitment, force generation and summation in muscles with elastic tendons (Nagamori, Laine, Loeb, & Valero-Cuevas, 2021). Even at the largely subconscious level of moment-to-moment corrections during a task, the nervous system seems always to be searching actively for improved performance. In the oculomotor system, the rate of adaptation to a change in the plant seems to be driven by such inherent trial-to-trial variability (Albert, Catz, Thier, & Kording, 2012), whereby the new cost of each trial drives the iterative process of adaptation, exactly as suggested above.
Distributed Control
In order to make use of the simplifying assumption of synergies or the analytical solution of optimal control, a single master controller is required to select and modulate the synergies or to compute the optimal commands to everything. This ignores the most basic anatomical facts about efferent pathways as grasped by Bernstein in 1935 (Figure 11): there are multiple controllers operating simultaneously on the same plant.
Figure 11
The pathways A-E represent the pyramidal, rubrospinal, vestibulospinal, and two tectospinal pathways. Reproduced from N. Bernstein, 1935, p. 111, with permission of the publishers.
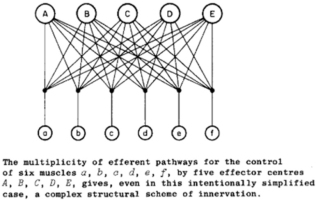
Bernstein assumed additive control at the spinal motoneuron as postulated by Sherrington’s final common path to the individual muscles (a-f in Figure 11), but he had little to say about what might be computed or controlled by the various inputs to that pathway. For the good-enough controller, the contributions of all other centers are simply part of the plant that each center is attempting to control. The addition of intermediary circuitry with computational functions of its own provides a basis for distributing sensorimotor control among the various efferent pathways and combining their results in a more useful way than a final common path. Simultaneous neural activity consistent with such integration has been recorded in motor cortex, pontomedullary reticular formation and spinal interneurons of non-human primates performing a finger dexterity task (Soteropoulos & Baker, 2020; Soteropoulos, Williams, & Baker, 2012).
From the perspective of one of the efferent pathways in Figure 11, for example the pyramidal tract from sensorimotor cortex, the other efferent pathways are invisible. If the outputs from the other pathways are deterministic, their effects look to the sensorimotor cortex like just another dynamic aspect of the plant through which it expresses its own commands. The job of sensorimotor cortex is to learn what outputs to the rest of the nervous system result in the desired sensory feedback (see Fig. 9). Such a computational function accommodates another inconvenient anatomical fact that is frequently overlooked: many of the efferent pathways project to other efferent pathways as well as to the integrative circuits of the spinal cord. For example, the sensorimotor cortex and the tectum project directly to the red nucleus, the vestibular nuclei and the pontomedullary reticular formation as well as to spinal cord. This means that the set of primitives that are controlled by any one efferent source includes all circuits to which it projects, which beggars the simplicity implied by calling them primitives (Giszter, 1992).
While the contributions of the various efferent centers of the brain may be deterministic, they are probably not static. Many centers appear to employ their own learning algorithms and/or reflect dynamic control by the cerebellum. The primate cerebellum contains over 50% of the neurons in the brain (Shepherd, 2004). It uses its own adaptive control rules to learn useful adjustments of the primitives embodied in the structures to which it projects directly (e.g. vestibular nuclei) or indirectly (via deep cerebellar nuclei). Direct cerebellospinal projections have recently been identified as important for learning coordinated limb movements (Sathyamurthy et al., 2020). Simultaneous adaptive plasticity in multiple controllers operating on the same plant presents obvious challenges to stability from an engineering perspective (Narendra, 2016), but somehow biological systems evolved to accommodate this robustly. This presents neurophysiologists and theoreticians with a challenge that needs to be investigated rather than denied or ignored by simplistic models of a singular cortical command center – the little man sitting in the control center of the brain.
Cortical Encoding
We should not expect the activity that can be recorded in any of the efferent pathways to align with the sorts of simple physical parameters used by engineers and physiologists to describe behavior. Neurophysiologists have identified correlations between motor cortical activity and parameters such as end-point force (Evarts, 1968), end-point velocity (Georgopoulos, Schwartz, & Kettner, 1986), and activation of individual muscles or groups of muscles that might reflect control of synergies (Todorov, 2000). This has led to claims that such canonical physical parameters represent the coordinate frame for commands computed by the motor cortex. As Bernstein pointed out, however, the muscles, bones and joints that constitute the musculoskeletal system are mechanically linked to each other. Forces and movements are not independent and neural activity recorded in one center may reflect its own efferent commands, efferent copy from other command centers and/or sensory feedback of forces or movements from the plant. It will always be possible to find correlations between neural activity in higher sensorimotor centers and almost any measurements of performance (G. E. Loeb, Brown, & Scott, 1996; Scott, 2000), but correlation is not causation. This presents a problem for experimental falsification of any theory of sensorimotor control by an appeal to typical neurophysiological data.
If a neural network learns a good-enough program to perform a task involving sequential recruitment of various muscles, what neural activity would be observed during its execution? Such a program would be essentially a learned version of the primitive, preprogrammed strategy of a central pattern generator (CPG). In a CPG, the neural activity responsible for each phase of the task drives the next phase; sensory feedback from the ongoing movement can modulate a CPG but it is not required for it to sequence through phases. An observer would find that the neural activity at any moment is best predicted by the neural activity from the previous moment rather than any aspect of the resulting behavior of the plant. The engineering term for this is rotational dynamics. Such activity has been found in primate motor cortex and it is produced by artificial neural networks trained to perform similar tasks; for recent results and review see (Kalidindi et al., 2020).
General Conclusions
We have now come full circle to a fundamental difference between engineered control systems and biological control systems. For an engineered system with unlimited bandwidth and negligible transmission delay, the best control scheme is complete centralization, in which one central controller receives and integrates all sources of sensory information and computes explicit commands to each actuator. Schemes for biological control that are derived from engineering control theory tend to start with this assumption and then add constraints and simplifying assumptions such as synergies and local servocontrol to make the problem more tractable computationally (G. E. Loeb, 1983). Real biological control evolved from and incorporated highly distributed and remarkably effective controllers such as those still found in invertebrates such as cockroaches (Büschges, 2005) and octopuses (Godfrey-Smith, 2017); see (Madhav & Cowan, 2020) for a recent review of the implications of such differences for control theory.
As animals became larger and more mechanically complex, biological systems gradually evolved to handle longer delays and larger numbers of sensory and motor signals. Those are the conditions for which engineered systems begin to use hierarchical control (G. E. Loeb, Brown, & Cheng, 1999), such as the fast, local servocontrol loops that stabilize the behavior of individual motors in robots. The existence of spinal reflexes and the identification of circuits that at first looked homologous to such servocontrol provided support for the notion that yet other engineering tools such as inverse dynamic analysis, system identification of internal models and optimal control might provide a theoretical basis for the rest of the biological control problem. In fact, the details of the circuits that have been elucidated in spinal cord and the many other distributed centers that contribute to sensorimotor integration look nothing like servocontrol. More modern engineering tools like linear quadratic regulator design and optimal feedback control make better predictions about biological circuitry and performance, but they are based on computational algorithms that are unrealizable in biological development and learning. Theories of biological control based on currently available control theory from engineering are metaphors built on quicksand.
Successfully evolved humans and well-engineered anthropomorphic machines can be expected to exhibit similar behavior because it is a requirement of their success. Engineering tools to analyze that behavior can identify the nature of the similar problems that must be solved by each (as first applied by Bernstein) and an understanding of why humans, computational models and robots might arrive at behaviors that appear to be similar. In order to understand how biological systems learn to perform such behaviors, we need computational models that reflect biologically plausible mechanisms for development and learning throughout the life of individual organisms, as well as their evolution in the first place. Such models and a theoretical understanding of how they work remain elusive.


