Introduction
The sprint step kinematics at maximum speed has been investigated in numerous studies without reaching a consensus for all variables (Bezodis, 2012; Debaere et al., 2013; Manzer et al., 2016; Mero et al., 1992; Young, 2007). Measuring elite athletes at their top level could lead to a better understanding of the relationship between maximum sprinting speed and sprint kinematics. At major international events data acquisition for scientific analysis is either severely limited to few variables or, in some cases, not possible at all. Normally video recordings are only available with limited frame rates, in which only the stride length can be accurately represented, but the temporal structure in addition to relevant sprint strike phases or body positions are inaccurately represented.
Therefore, studies with elite sprinters are necessary, close to the international championships based on a sprint technique model. The “Swing-Pull Technique” model, which was based on the findings of electromyography research (Wiemann and Tidow, 1995), is assumed to be a suitable model for kinematic analysis. The model divides the sprint step into the swing and pull phases and further sub-phases related to the sprint performance. The new kinematic model which uses these phasing structures (t1-t8) subdivides the phases into four sub-phases (swing-off, forward (knee lift) swing, pre-support and support) that represent performance of the sprinter (swing-off, heel to the buttock, etc.) (Figure 1). The events t1 and t8 mark the toe-off and thus the beginning and the end of the sprint step. The other events are determined by extreme values (minima and maxima) of the knee or hip angle.
Figure 1
Phase structure of the “Swing-Pull Technique” with their actions (second row) of the highlighted leg (black)
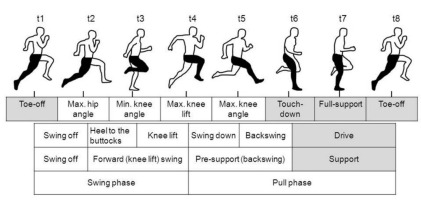
The kinematic model of the “Swing-Pull Technique” depicts the down- and backswing during the pre-support and the drive during the support (ground contact). Both phases are characterized by fast hip extension. A shorter contact time can be achieved by high hip extension, high backswing velocity of the foot before ground contact as well as low knee flexion and extension during the support phase. The pre-support is prepared by the knee lift swing with rapid hip flexion and a high knee position before the downswing as well as a quick change of hip flexion in hip extension without rest. Consequently, the angles in the knee and hip joint at the eight key positions (t1 - t8), the hip flexion and extension angular velocity (during knee lift swing and pre-support), as well as the backswing velocity of the foot before ground contact are important kinematic features of the “Swing-Pull Technique”.
Kinematic features which have been demonstrated to be related to maximum sprinting speed are the step rate and stride length. Maximum sprinting speed is a result of an optimal relationship between the step rate and stride length (Schiffer, 2009). Analysis of a 100-m sprint showed that the step rate reached its maximum value after 10 – 20 m (Haneda et al., 2002), and it would remain constant throughout maximum sprinting speed (Ito et al., 2006), eventually decreasing during the final stages of the 100-m dash (Coh et al., 2010; Mero and Peltola, 1989). In contrast, the stride length reached highest values later between 50-80 m (Graubner and Nixdorf, 2011; Ito et al., 2006) and increased at the last stage of the 100-m sprint (Chatzilazaridis et al., 2012; Mero et al., 1992). For intermediate to advanced performance-level athletes, stride length is viewed as the main factor for the production of maximum speed (Kumar, 2006; Mackala, 2007).
Short ground contact time, which is another kinematic feature, is crucial for high sprinting speed which requires the sprinter to produce a great amount of force in a short period of time (Mann, 2011; Mero et al., 1992; Nummela et al., 2007). Other kinematic features such as an active foot contact with fast backswing velocity of the foot before ground contact (Mann and Sprague, 1983; Hay, 1994; Wood, 1987), a small horizontal foot distance from the center of mass at foot contact (Mero et al., 1992), fast hip extension speed before the landing (Mann et al., 2008), and small knee flexion in the support leg during support (Hunter, 2005) could contribute to minimizing the breaking impulse which is related to the maximization of sprinting speed.
The aim of the present study was to empirically verify the “Swing-Pull Technique” model with data collected from the German national sprinting teams. The relationship between sprinting speed and kinematic features of the sprinting technique was examined via correlation analysis. The following hypotheses were tested: 1. the higher the sprinting speed, the greater the stride length and the shorter the ground contact time 2. higher sprinting speed would correlate with:
a faster hip flexion angle velocity during the knee lift (t3-t4),
a higher knee position at the end of the knee lift (t4),
a faster vertical foot velocity and hip extension velocity during the pre-support (t4-t6),
a foot ground contact near the vertical projection of the trochanter major at the take-on (t6), and
smaller knee flexion followed by smaller knee extension during the support phase (t6 - t8).
Methods
Participants
Participants (German Track and Field Association athletes) completed 30-m flying sprints at maximum sprinting speed on a tartan track. In total 26 elite male sprinters participated in this study (Table 1). The time of the evaluations was approximately three weeks prior to the seniors’ and U20 juniors’ competition (World or European Championships 2014, 2015, and 2016). The test procedures were in accordance with the Declaration of Helsinki, 1975. Data collection was part of a routine diagnosis in agreement with the German Track and Field Association.
Table 1
Participants’ characterisics, mean ± standard deviation
Design and Procedures
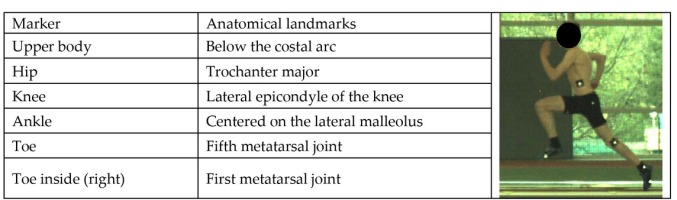
The study was conducted as field testing during training sessions. Evaluations took place at two different locations in Germany (“Kienbaum National Olympic Training Centre”) and Spain (“Estadio Olímpico Municipal Antonio Domínguez in Playa de las Americas”, Tenerife) in order to recruit a sufficient number of sprinters. Athletes completed their warm-up with their own individual program. A general warm-up with running shoes which lasted 20 min included slow running, dynamic and static stretching exercises, and various 40-m drills like high knees, kicking heels backwards, etc. After the general warm-up visible markers were applied to athletes using a six-point lower extremity body model (Figure 2). Next, athletes completed a specific sprint warm-up with spikes, which lasted 20 min, and that comprised 40-m drills with high intensity, sprints over 40-60 m with gradually increasing speed and acceleration sprints over 10-20 m. Then two 30-meter flying sprints at maximum speed with a rest interval of at least 20 min followed. In a two-dimensional kinematic analysis, a single sprint stride of the fastest sprint was chosen for further evaluation.
Measures
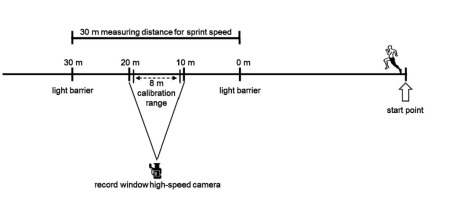
For each athlete a sprint stride was recorded from the sagittal plane by means of a high-speed video camera (Photonfocus AG, Switzerland). Camera frequency was set to 200 Hz with an image of 1760 × 448 pixels. TEMPLO software (Contemplas, Kempten, Germany) was used for video acquisition. The camera setup is shown in Figure 3. Two hurdles equipped with vertical antennas (1 m) were positioned in the recording frame for calibration. The calibration area covered an 8 (width) by 1.80 m (height) space. For the kinematic analysis the sprint stride from event 1 (toe-off left) to event 8 (toe-off left) in the 10-m interval (10-20 m) was selected. The sprint time was recorded for a 30-m distance using a triple photoelectric barrier (Wilhelm Köster, Ditzingen, Germany).
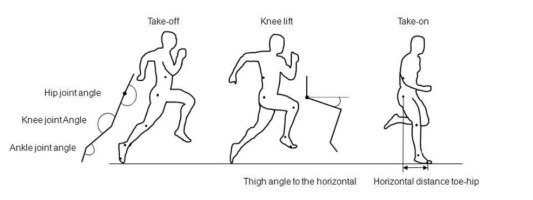
After importing videos from TEMPLO to Vicon Motus (10.1, Vicon Motion Systems, UK; CONTEMPLAS GmbH, Germany) raw data tracking was performed manually with “auto-advance point option”. Raw data were filtered using a digital first-order low-pass Butterworth (cutoff frequency of 10 Hz). Afterwards three joint angles (hip, knee, and ankle) and the angle between the thigh and a horizontal line (Figure 4) were calculated.
Toe-off (t1, t8) and touch-down (t6) events were determined in the recordings. The last image with ground contact was used for toe-off (t1), whereas the first image with ground contact was used for touch-down (t6). To visually identify ground contact events, compression of the shoe was used. Two researchers performed this identification. The events t2-t5 were detected by means of the minima or maxima of the calculated knee or hip angles.
Table 2 shows the definition and calculation of the kinematic variables used. In addition, three joint angles (hip, knee, and ankle) were calculated for the eight key positions. All markers were assumed to represent the joint centers (Figure 3). Possible reasons for the inaccuracy of the data might have been video calibration, parallax effects, and error propagation in the determination of the angular velocity.
Table 2
Definition and calculation of the kinematic variables
| Kinematic feature | Unit | Definition |
|---|---|---|
| Sprinting Speed | m/s | t30m/30 (t30m= time over 30 m) |
| Contact time (tc) | ms | tt8-tt6 |
| Flight time (tf) | ms | tt6-tt1 |
| Step rate | 1/s | 1/((tc+tf)/1000) |
| Stride length* | m | Half of the distance between the toe marker for two consecutive contact phases of the analyzed leg |
| Hip flexion angular velocity | °/s | Average hip flexion angular velocity between t3 and t4 |
| Hip extension angular velocity | °/s | Average hip extension angular velocity between t4 and t6 |
| Vertical foot velocity | m/s | Vertical maximal velocity of the toe marker between t5 and t6 |
| Knee joint flexion | ° | Knee angle at t6 minus minimal knee angle during ground contact |
| Knee joint extension | ° | Knee angle at t8 minus minimal knee angle during ground contact |
| Horizontal distance toe - trochanter major | cm | Horizontal distance between the toe and hip marker at ground contact |
The measurement accuracy of the temporal and spatial variables was estimated to be ± 5 ms for time, ± 1.5° for the angle, ± 45 °/s for angular velocity and ± 2.5 mm for the distance variables. The estimation indicated the maximum error and considered time and pixels resolutions of the video, the motion capture volume calibration deviations, parallax effects, and error propagation in the determination of the angular velocity.
Statistical Analysis
The relationship between sprinting speed and kinematic variables was determined using Pearson correlation. Normal distribution was assessed using the Kolmogorov-Smirnov test. The significant level was set at p ≤ .05. IBM SPSS 22 (Chicago, IL, USA) was used to conduct statistical analysis.
Results
Table 3 summarizes the data for sprinting speed, stride length, step rate, ground contact time, and flight time. The sprinting speed varied from 10.1 to 11.3 m/s.
Table 3
Sprinting speed and kinematic data of stride characteristics
Higher sprinting speed significantly correlated with shorter ground contact time and longer stride length, but did not correlate with the step rate and flight time (Table 4). An inverse relationship existed between the stride length and the step rate. It can be stated that the longer the stride length the smaller the step rate. Furthermore, longer step length correlated with greater flight time. A higher step rate resulted from smaller ground contact time as well as a smaller flight time (Table 4).
Table 4
Correlation coefficient (r) between sprinting speed and kinematic characteristics of sprinting speed
| Characteristic | Sprinting speed | Stride length | Step rate | Ground contact time | Flight time |
|---|---|---|---|---|---|
| Sprinting speed | |||||
| Stride length | .53** | ||||
| Step rate | .25 | -.67** | |||
| Ground contact time | -.53** | .21 | -.74** | ||
| Flight time | .13 | .78** | -.77** | .14 |
Table 5 depicts the measured values for the kinematics of sprinting technique and their correlation to sprinting speed. Maximum sprinting speed was strongly correlated with smaller extension in the hip (r = -.51; p = .007), knee (r = -.52; p = .005), and ankle (r = -.52; p = .006) joint at the take-off, faster hip extension velocity (r = .63; p = .001) and vertical foot velocity (r = .77; p < .001) during the backswing phase, as well as smaller knee flexion (r = -.54; p = .005) during the ground contact phase. Furthermore, there were moderate correlations between maximum sprinting speed and greater knee extension (r = .40; p = .038) at the maximum knee angle and a greater horizontal distance from the toe to the trochanter major (r = -.41; p = .035) during pre-support as well as a smaller ankle angle (r = -.43; p = .032) at the take-on.
Table 5
Mean ± standard deviation and 95%-CI for the sprint technique characteristics and correlation with sprinting speed
Discussion
The correlation analysis included data from elite sprinters with sprinting speeds ranging from 10.1 to 11.3 m/s. The range of measured values can be explained by the composition of participants, whereby seniors were recruited from the top national 100 m and 200 m sprinters, and the juniors U20 from the national 100 m - 400 m teams.
Although a margin for improving sprinting variables exists for each individual, the data range for seniors was smaller. The data range characterizes the application scope of the correlation results. In this sense it is important because in a heterogeneous sample the probability of finding a significant relationship between the measured variables is higher compared to a homogeneous group. In order to present valid findings for the stride kinematics at a high sprinting level, only data from the flying sprint with a velocity higher than 10.1 m/s were selected.
As hypothesized, higher sprinting speed correlated with longer stride length as well as shorter ground contact time. The higher the sprinting speed, the longer the stride length and the shorter the ground contact time. Conversely, the step rate and flight time had no relationship with maximum sprinting speed.
The results indicate that the short ground contact time of less than 100 ms is a characteristic feature of a sprint at maximum speed (Mann, 2013; Mero et al., 1992; Nummela et al., 2007). The fastest sprinter reached a ground contact time of 85 ms. Corresponding with previous studies the intermediate and advance performance level of the maximum sprinting speed can be determined via stride length (Kumar, 2006; Mackala, 2007; Mero et al., 1985). Just as the results indicate, the long step does not necessarily prolong the ground contact time. Stride length and ground contact time are determined through sprinting technique and other factors (height and leg length) as well as reactive strength (Majumdar and Robergs, 2011). The measured stride lengths from 2.32 ± 0.11m are comparable with other studies with elite athletes in the intermediate division. A stride length of 2.48 ± 0.08 m at the average sprinting speed of 11.8 ± 0.23 m/s was measured at the 60-80 m stage for the finalist participants of the 2009 world championships (Mackala and Mero, 2013). In contrast, a stride length of 2.15-2.25 m was found for elite sprinters (Salo et al., 2011).
A higher step rate correlated with both shorter ground contact and shorter flight time. The fundamental importance of a shorter ground contact time, which significantly contributes to a higher step rate, is discernable. In contrast, no correlation was identified between ground contact time and flight time. An inverse relationship exists between stride length and the step rate which has already been reported in previous studies (Hay, 1994; Kunz and Kaufmann, 1981). Consequently, the fast sprint at maximum speed can be characterized by a longer stride length and shorter ground contact time.
A higher sprinting speed was associated with different characteristics of the “Swing-Pull Technique”. As it was assumed in the hypothesis, sprinting speed correlated with smaller knee flexion and hip extension during ground contact (t6-t8), with a smaller knee angle at the take-off (t1), with faster hip extension velocity and vertical foot velocity at pre-support. Thus, the correlation analysis confirms the performance relevance of technical characteristics, which has also been verified in previous studies. A flat active foot contact (Seagrave et al., 2009; Young, 2007) with faster backswing velocity of the foot before the take-on (Hay, 1994; Mann and Sprague, 1983; Wood, 1987), faster hip extension velocity at the take-on (Mann et al., 2008), and a smaller range of motion of the knee joint during the ground contact phase (Hunter, 2005) were confirmed. A non-fully extended knee at the take-off has already been identified as a kinematic characteristic of a modern sprinting technique (Bezodis et al., 2008; Wiemann and Tidow, 1995).
Furthermore, a relationship was found between sprinting speed and a larger knee angle at maximum knee flexion (t5), a longer horizontal foot-to-body distance, and a smaller ankle angle at the take-on (t6) which was not expected.
The expected relationship between sprinting speed and a smaller horizontal foot-to-body distance at foot contact was not established, hence results of the previous studies cannot be confirmed (Mero et al., 1992). In contrast, the faster sprinters executed a longer foot-to-body distance at foot contact. It should be noted that horizontal value of the metatarsophalangeal joint of the small toe to the perpendicular projection of the trochanter major was selected. The actual position of the body’s center of mass was not taken into account.
A smaller flexion angle in the knee in addition to smaller knee-to-hip extension during ground contact appears to be essential for producing ground contact time under 100 ms. Thereby, shorter ground contact time is not sufficient for pronounced knee extension. Focus should lie on a reduction of the knee flexion and fast hip extension during ground contact.
The used kinematic analysis model is oriented towards the “Swing-Pull Technique” (Wiemann and Tidow, 1995) and illustrates the key positions as well as phase structures of maximal sprint adequately. Continuous hip extension was shown during the pre-support and support phases. This finding highlights the importance of hip extensors as the main driving muscle for the production of maximum sprinting speed (Wiemann and Tidow, 1995). Hip extension started from the maximum knee lift (t4) subsequent to pre-support (t4-t6) up until the take-on. During ground contact (t6-t8) this active hip extension continued and ceased only after the take-off with the maximum hip angle at t2 (Wiemann and Tidow, 1995).
The interpretation of the relationship between sprinting speed and kinematic stride characteristics must consider their different elevation as a limitation. Sprinting speed was calculated as an average of a 10-m distance using the time measured with a triple photoelectric barrier. However, only one step of the 10-m distance was analyzed.
Conclusion
The correlation analysis confirmed the effect of stride length and ground contact time for the production of maximum sprinting speed on the examined athletes. Having said this, at comparable sprinting speed, a scope of individual relationships between stride length and the step rate remains dependent on anthropometric features, strength, and coordinative abilities. While training, the inverse relationship between the step rate and stride length as well as the athlete’s personal preference should be taken into account. With this in mind a distinct training goal can be set, which follows different adaptations. Optimal training for maximum sprinting speed requires a personalized approach to optimize the relationship between stride length and the step rate.
The use of kinematic characteristics of the “Swing-Pull Technique” analysis was confirmed for sprints. The characteristics should primarily be taken into account in conditioning, coordination, and technical training. For maximum sprinting speed, fast foot contact speed, small knee flexion associated with small knee extension during ground contact, fast hip extension speed during knee lift swing, and fast hip extension speed during the pre-support phase are necessary.