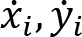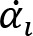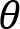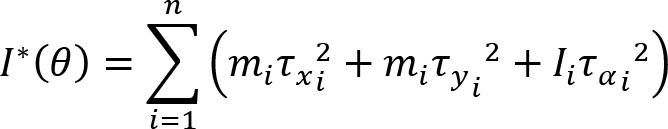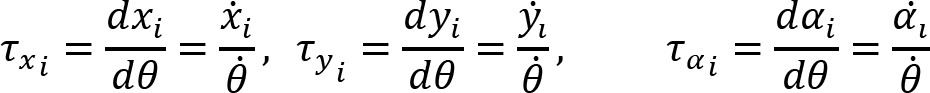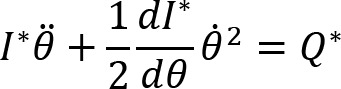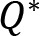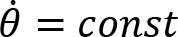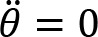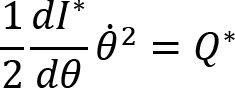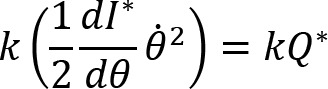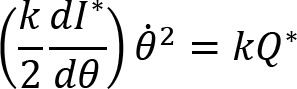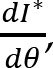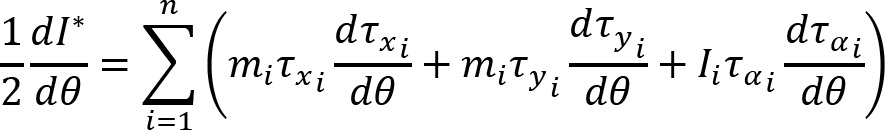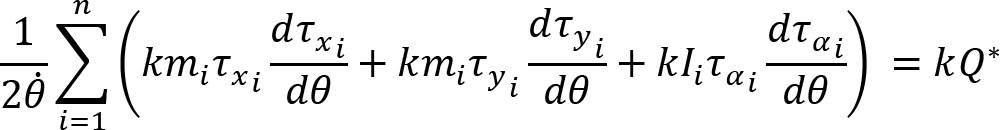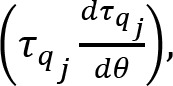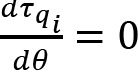Introduction
Arm cycling on arm ergometers is often applied in sports training when the aim is to strengthen upper body muscles in neurologically intact individuals (Elmer, Danvind, et al., 2013) or to assess muscle powers and evaluate performances (Hübner-Woźniak et al., 2004). Arm cycling exercises are also included in medical rehabilitation protocols (Zhou et al., 2018) to improve motor performance and motor control of individuals with spinal cord injury or stroke (Lasko-McCarthey and Davis, 1991; Zehr et al., 2012). These exercises are also used in combination with functional electrical stimulation (FES) training of individuals with spinal cord injuries. (Brurok et al., 2013; Bakkum et al., 2015) Despite a range of sport and rehabilitation applications (Elmer, Marshall, et al., 2013; Matjacic et al., 2014), the literature on arm cycling movements is limited relative to that on lower limb cycling. However, the importance of arm cycling has recently been supported by several investigations. The influence of arm cycling at various cadences on the modulation of supraspinal and spinal excitability of the biceps brachii (Forman et al., 2015) has been demonstrated and data indicated an increase of excitability of corticospinal neurons as arm cycling cadence increased. The power output also affected the corticospinal excitability of arm muscles (biceps brachii and triceps brachii) during arm cycling (Spence et al., 2016; Lockyer et al., 2018).
Regarding interlimb coordination, particularly interlimb reflex modulation, it was shown that arm cycling suppresses H reflex amplitude in soleus muscles and bilateral and unilateral cycling yielded equivalent suppression (Loadman and Zehr, 2007) and no significant differences were seen in the level of suppression of the H reflex at different crank loads (Hundza et al., 2012).
It was supported by data, that neural coupling between the arms helps to increase movement symmetry and to ensure stable arm cycling (Vasudevan and Zehr, 2011). It has also been shown that arm cycling training improves strength, coordination of muscle activity during other types of motor tasks, such as walking, and neurological connectivity between the arms and the legs (Kaupp et al., 2018).
Altogether, these studies highlight the importance to explore upper limb cycling from biomechanical and motor control aspects as well.
Arm cycling is an interesting task because it offers the combination of a redundant, yet constrained movement. The hands are constrained to move along a given circular path. While the trajectory followed by the hand is constrained, the arm joints could follow a myriad of trajectories. Thus, the same hand trajectory is associated to a succession of ever-changing, and not necessarily repeatable, arm poses. The constrained hand trajectory is often performed at a specified cadence, against a set resistance. Given a cadence, an increase in crank resistance is known to require an increased muscle activation. Arm muscle activities during arm cycling at different workloads were characterized in (Chaytor et al., 2020) and it was found that there was a linear relationship between EMG amplitude and power output for individual muscles. On the other hand, an increase in muscle activation also produces an increased signal dependent motor noise. This motor noise can be a source of variability for the muscle activation and of the arm pose as well.
Our goal was to examine how the crank resistance influences the variances of joint configuration and muscle activation. There is literature in robotics about control of manipulators where the movement of the end-effector is constrained, but the load on it is changed (Mason, 1981; Khatib, 1987). This literature offers models for accomplishing the task. Our particular purpose was to analyze the physiological parameters of human subjects during arm cranking when an altered load is applied (effect of crank resistance). The metrics we analyzed are the joint configuration variance (in 3D joint space) and the muscle activation variance (in 4D muscle activation space). These metrics can indirectly validate the type of control utilized for this complex task.
As stated above, repeating in each cycle the same joint configuration sequence as the resistance of the crank increases is not guaranteed. It has been demonstrated that, for a constrained movement, the joint stiffness increases as the load at the end-effector increases (Osu and Gomi, 1999). Changes in joint stiffness at each joint can substantially change the pose of the arm even though the endpoint trajectory is unchanged. Following the Passive Motion Paradigm (Mohan and Morasso, 2011) the joint stiffness is changed in order to control the end effector load. If the joint configuration variance is not affected by crank resistance, it suggests the separation of kinematic- and force-control (Kolesnikov et al., 2011; Piovesan et al., 2019) where the kinematic task can be maintained safely when crank resistance is altered. Knowing the type of control strategy is important in training and rehabilitation protocols. It is not the aim of this paper to evaluate rehabilitation protocols, but to provide a validation of the already developed theories applied in robotic rehabilitation (McIntyre et al., 1995; Chib et al., 2009; Squeri et al., 2010).
In the present exploratory study, we investigated unimanual and bimanual arm cycling, focusing on motor variance at the joint and muscle levels. Cycling was performed on an ergometer against three crank resistances. The aim of the study was to assess the effect of external load on variances in joint coordination and muscle coordination. This would help to reveal if there exists a mechanism for the concurrent control of motion and force, and to which extent the two can be controlled separately in arm cycling.
Methods
Participants
Fifteen right-handed, able-bodied participants (24 ± 4 years old) were recruited in the study who performed arm cranking movements on an arm cycle ergometer. The study was approved by the Ethics Committee of the National Institute for Medical Rehabilitation, Budapest, Hungary. Written informed consent was obtained from all participants, and they participated voluntarily in the study.
Experimental setup
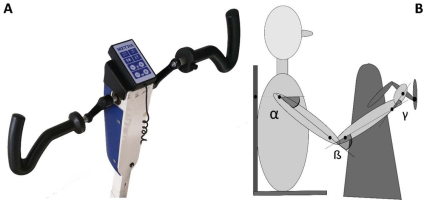
Each participant was seated in a fixed chair in front of an arm cycle ergometer (MEYRA, Kalletal, Germany (Fig. 1). The participant grasped the handle of the ergometer at the end of the crank, which was 10 cm long. The distance between the chair and the ergometer was set in such a manner that when the handle of the ergometer was at the most distant position with respect to the participant, the external angle of the elbow (the angle of the forearm with respect to the elongation of the long axis of the upper arm) was approximately 10-15 degrees. This corresponded approximately to the most extended elbow position. This angle was measured with a protractor. The shoulders were strapped (with a chest strap) to the back of the chair to restrict the movement of the trunk. Note that because of the difference in participant size this configuration does not guarantee that each participant moves with the same angular displacement. For that case, the dimension of the crank would have need to change from participant to participant. Nevertheless, the subject dependent variation has been taken into account within our statistical analysis, considering the subject as a random factor.
Figure 1
Equipment and maker positions. A: arm cycle ergometer. B: schematic figure of the cycling participant. Black dots illustrate positions of markers placed on the body, on the handlebar of the ergometer and on the chair on which the participant was seated. Joint angles in the shoulder, elbow and wrist, respectively, were computed from marker coordinates.
Ultrasound emitting markers as part of an ultrasonic movement analyzer system (ZEBRIS CMS HS, Isny, Germany) were placed on anatomical landmarks. In particular, we used markers of the following landmarks: acromion, distal end of the humerus, proximal end of the ulna, styloid process of the ulna, caput of metacarpal of the fifth digit. One marker was placed on the chair and one on the handlebar of the ergometer. The positions of the markers were recorded by three ultrasound-sensitive microphones, with a sampling frequency of 100 Hz.
The surface EMG activity was recorded by the EMG recording apparatus of the ZEBRIS system, from the right and left biceps (BI), triceps (TR), deltoideus anterior (DA), and deltoideus posterior (DP) muscles, with a sampling frequency of 900 Hz. The skin was dry shaven and cleaned with 70% alcohol before placing pairs of NORAXON (Type 272) electrodes (interelectrode distance was 1.5 cm). The positions of the electrodes were based on the recommendations of the SENIAM project, “Recommendations for sensor locations on individual muscles” (Hermens et al., 1999). A reference electrode was placed at the elbow (over the olecranon).
Motor task
The participant was instructed to cycle with a cadence of 60 revolutions per minute (rpm), against three different crank resistances: low (1), moderate (2) and high (3). Cycling was performed bimanually and unimanually with the left or right arm. The resistance was quantified as the torque with which the crank resists rotation. In unimanual cycling, the low, moderate and high resistances were 1.16 Nm, 2.08 Nm, and 3.09 Nm, respectively. In bimanual cycling, they were 1.16 Nm, 3.09 Nm, and 6.14 Nm, respectively.
Cycling was performed by each participant unimanually (by the left and right arm) and bimanually under each of the three resistance conditions. Note, that we have tried to maintain the change in load between condition somewhat constant, assuming that the in the bimanual task the load is split in two. Some limitation in proper distribution of the load between conditions comes from the pre-set resistance of the ergometer.
The palm was positioned horizontally, with the forearm pronated, and the fingers were bent around the horizontal handle. The order in which cycling conditions were chosen was random. In each condition, the participants cycled for 30 seconds. They had 1 minute of rest between conditions. A metronome was used to guide the participants to keep the cadence of 60 rpm.
Data processing and analysis
Recorded EMG signals of each muscle were filtered using custom software in MATLAB (Mathworks, Natick, MA). Frequencies below 25 Hz and above 300 Hz were cut off (4th order Butterworth bandpass filter), as were frequencies from 49-51 Hz to eliminate the effect of the electrical power source (i.e. 50 Hz in Europe). After filtering, a root mean square (RMS) algorithm was applied to smooth filtered signals with a moving window of 0.088 ms (80 samples).
Muscle activation was represented, at each instant (t), in a 4-dimensional muscle space by a 4-dimensional vector M(t), whose coordinates were the EMG amplitudes of the four measured muscles:
Recorded marker coordinates were filtered applying discrete cosine transformation (DCT) to eliminate artifacts (Shin et al., 2010). Here, DCT was used to transform the recorded kinematic signals from the time domain to the frequency domain. Then, we multiplied the results with a 3rd order low-pass Butterworth gain function (cutoff frequency 10 Hz). Finally, inverse DCT was applied. The intersegmental angles at the shoulder, elbow and wrist were computed from filtered marker coordinates by trigonometric equations. Fig. 1 illustrates the joint angles: shoulder – α, elbow – β, wrist – γ. Joint configuration was represented, at each instant (t) in a 3-dimensional joint space by a 3-dimensional vector
Arm cranking is often represented as a planar movement in the sagittal plane, where the crank angular velocity is defined as a vector orthogonal to such a plane. We are aware that the movement is not completely planar, in the sense that there is a small ab-adduction angle at the shoulder and thus the elbow may deviate from the sagittal plane. However, the direction of the angular velocity of this rotation passes through the instantaneous center of rotation of the shoulder and the point of contact of the hand and crank. As described in publications illustrating the Uncontrolled Manifold (Scholz and Schöner, 1999), the variance of this degree of freedom does not influence the main task since the angular velocity vector of the crank and the angular velocity vector of the ab-adduction angle, are always orthogonal. We define the osculating plane ”Os(t)” as the plane orthogonal to the angular velocity around the elbow. Within this plane, we consider 3 degrees of freedom: elevation of the shoulder (α(t)), flexion-extension (β(t)) of the elbow, and flexion-extension of the wrist (γ(t) ).
Variance calculations
Time courses of joint angles
Then, angular variances (joint configuration variances) and muscle activity variances across cycles were computed at each percentage of cycle time.
Joint configuration variance per degree of freedom was defined by the following equation:
where
Similarly, the muscle activity variance per degree of freedom was defined as:
where M(t) = [BI(t), TR(t), DA(t), DP(t)] and t = 1, … ,100 (percentage of cycle time).
Variances of either the angles or the EMG signals
Statistical methods
We calculated a multiple ways mixed factor analysis of variance (ANOVA) for both the variance norm of angles and surface Electromyographic signals. In the analysis we considered 4 factors such as side=[‘left’,’right’], mode = [‘Double’,’Single’], loading resistance = [’Level 1’, ‘Level 2’, ‘Level 3’], and the [subject] which should be considered as a random factor and therefore makes this a mixed model. We also included in the model both a pairwise and a three-way interaction between the factors. The standard deviation for the whole population of angle variances is the linear sum of the standard deviation due to each factor. Thus, by doing a multifactorial ANOVA we can pinpoint the size of the standard deviation for each factor and see which one makes us reject the null hypothesis. A post-hoc multicompare analysis based on Tukey's honestly significant difference criterion was also performed.
Results
Neither the factors nor their interaction with each other creates a significant difference for the joint configuration variance. On the other hand, we can observe a significant effect of both the loading resistance
Kinematic variances
Crank resistance (CR) did not have a significant effect on angular variances (F2,28=1.43, p=0.2573) Furthermore, the interaction between load and cycling mode was also not significant (F2,28=0.28, p=0.7574) (Fig. 2 A1 and A2). Side (F1,14=1.20, p=0.2910) and cycling mode (F1,14=0.5, p=0.4894) did not have a significant effect on angular variances (Fig. 2B and 2C).Joint configuration variances (as functions of normalized time) were compared for low, moderate and high CRs (Fig. 3).
Figure 2
Mean joint configuration (angular) variances A1) in low, moderate and high resistance conditions for bimanual cycling (mean across participants and sides); A2) in low, moderate and high resistance conditions for unimanual cycling (mean across participants and sides). B) in bimanual and unimanual cycling (mean across participants, resistances and sides); C) in left and right arms (mean across participants, resistances and modes). Lines above bars denote standard errors of the mean (SEM).
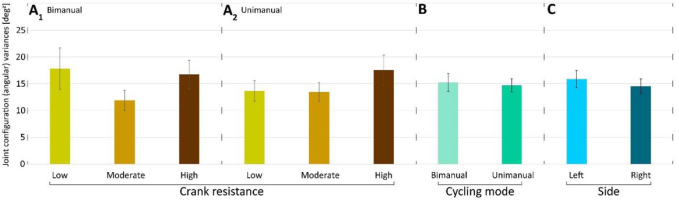
Figure 3
Joint configuration (angular) variance profiles. Time course of angular variance
Dotted line: Mean+SEM
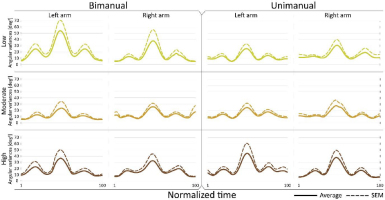
Fig. 2 and Fig. 3 show that the magnitude of joint configuration variances and the time profiles of angular variances were not significantly affected by crank resistance. This was observed in both bimanual and unimanual cycling. Note, that the variance has three peaks. Since the cadence is constant there is a monotonic mapping between time and the angular position of the crank. Thus, the peaks occur approximately at position 90º, 180º, and 270º, of the crank angle, where the maximum variance is at 180º where the arm is fully extended, and where the kinetic energy of the arm is maximum.
Muscle activation variances
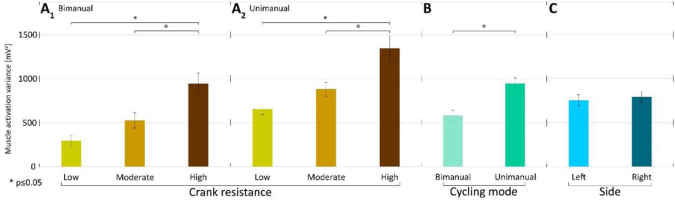
Higher crank resistance was associated with higher muscle activation variances (Fig. 4 A1 and A2) in all examined cycling conditions for both arms. This difference was significant when low and high crank resistance conditions were compared in either bimanual (p<0.0001) or unimanual cycling (p<0.0001) according to a post-hoc multicompare analysis based on Tukey's honestly significant difference criterion. This was also true when moderate and high crank resistances were compared in either bimanual (p<0.00025) or unimanual cycling (p<0.0001). Comparing bimanual and unimanual cranking, the muscle activity variance was higher for unimanual than for bimanual cranking (Fig. 4 B). Comparison of muscle activation variances when cranking by the left and right arm did not show significant difference (Fig. 4 C).
Figure 4
Mean muscle activation variances A1) in low, moderate, and high resistance conditions for bimanual cycling (across participants and sides); A2 ) in low, moderate, and high resistance conditions for unimanual cycling (across participants and sides); B) in bimanual and unimanual arm cycling (mean across participants, resistances, and sides F=20.11, p=0.0005); C) in left and right arms (mean across participants, resistances and modes F=0.15, p=0.7062); Lines above bars denote standard errors of the mean.
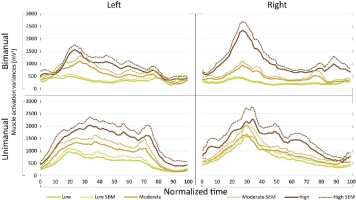
In addition to comparing average muscle activation variances, muscle activation variance profiles were also compared among various cycling conditions. It was found that the shape of the variance profiles did not change for the specific arm, only its magnitude changed according to crank resistance. This finding is presented in Fig. 5.
Figure 5
Muscle activation variance profiles. Time course of muscle activation variance
To represent quantitatively the similarity of the variance profiles, we computed correlation coefficients of the variance curves obtained in
different resistance conditions. High correlations were observed when comparing variance curves, presented at Fig. 5, for different cranking conditions in unimanual cranking for both arms and bimanual cranking for the right arm. A weaker linear correlation was found between variance curves observed in bimanual cranking for the left arm (Table 1).
Table 1
Correlation coefficients of mean muscle activation variance time courses.
| Bimanual | Unimanual | |||
|---|---|---|---|---|
| Left arm | Right arm | Left arm | Right arm | |
| low and moderate | 0.51 | 0.77 | 0.95 | 0.96 |
| low and high | 0.35 | 0.77 | 0.89 | 0.93 |
| moderate and high | 0.90 | 0.92 | 0.98 | 0.93 |
[i] Mean muscle activation variance time courses (VEMG(t)) were correlated based on different resistance conditions (low, moderate, high). Correlation coefficients between 0.40 and 0.59 were defined as ‘moderate positive correlation’, between 0.60 and 0.79 were defined as ‘strong correlation’, and between 0.80 and 1.00 were defined as ‘very strong correlation’.
Naturally, if muscles are working against higher external resistance, the EMG amplitudes increase, thus the magnitude of muscle activation vector increases. On the other hand, the profile of the muscle activation does not necessarily need to remain the same, but we can reveal that it does within the same arm/condition. If the amplitude increases in such a manner that the signal with lower values is simply multiplied by a constant c>1 then the variance will be multiplied by c2. The result is not trivial because for this to happen, the control variable needs to be linear (Kaupp et al., 2018) , and the system to be controlled is highly nonlinear. Indeed, the force of each muscle (and the activation signal that mediates it) is required to accomplish 3 distinct tasks. These tasks are 1) providing the operational command for the hand to follow the prescribed trajectory, 2) compensating non-inertial forces such as centrifugal and Coriolis forces that are generated by the nonlinear dynamics as a result of the movement and, 3) generating additional forces for matching the resistance. Thus, for the variance to change quadratically between load conditions the controller must be able to decouple these components to guarantee that the operational task remains the same and that the resistance force is matched. We investigated how the magnitude of muscle activation and the variance of muscle activation increased when crank resistance increased. We found that the variances changed almost quadratically with respect to the change in average muscle activation. Fig. 6. presents that the average variance of muscle activation increases approximately at the same rate as the mean squared muscle activation when the crank resistance is increased.
Figure 6
The ratios of average variances of muscle activations compared to the squares of the ratios of average muscle activation magnitudes. A) The ratios of variances in moderate crank resistance respect to variances in low crank resistance and the squares of the ratios of average muscle activation magnitudes in moderate respect to low crank resistance; B) The same as A when the ratios are computed in high respect to low crank resistance. Ratios are presented for different combinations of conditions separately (left arm bimanual, left arm unimanual, right arm bimanual, right arm unimanual). Mean and standard errors across participants are presented.
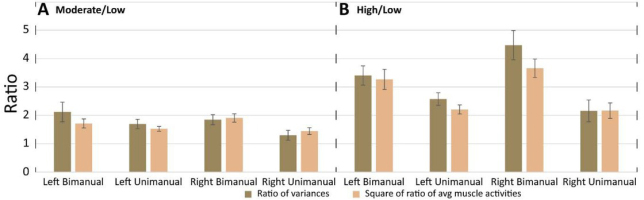
For each participant, the average magnitude of muscle activation across time was computed for moderate and low crank resistances separately. The average obtained for moderate resistance was divided by the average that was obtained for low resistance. Thus, we get one ratio for each participant. The squares of this ratios were averaged across participants and these average values are presented at Fig 6 for different conditions (bimanul/unimanual, left/right arm) separately. The same method was used for the computation of the square of ratios of magnitudes of muscle activation obtained for high resistance with respect to magnitudes of muscle activation obtained for low resistance.
The ratios of variances of mucle activations in moderate crank resistance to variances of muscle activations in low crank resistance, and the ratios of variances muscle activations in high respect to low crank resistance were also computed and presented. We compared the ratio of variances and the square of ratio of muscle activation magnitudes applying paired sample t-test, (p=0.05). There were no significant differences in any cycling conditions (Fig. 6.).
Discussion
Arm cranking is a cyclic and constrained movement. Considering cyclic arm movements, such as circle drawing, variances have been studied with regard to the endpoint trajectory and joint configuration (Verschueren et al., 1999; Tseng and Scholz, 2005; Tseng et al., 2006; Dounskaia, 2007; Keresztényi et al., 2009). When arm cranking on an ergometer, not only the fixed hand path is given that has to be tracked by the endpoint of a multijoint system, but there is also the need to produce an additional force. Equations for closed chain mechanisms, which show that both torque and angular position must be controlled is presented in the appendix (based on the approach given in (Yagiela et al., 2020). These formulas show that the variance of the angles must change unless another control mechanism is taking place.
Even if the desired hand path is given or it is fixed, there is still flexibility to choose patterns of joint coordination and muscle activation. However, our results suggest that neural control maintains the same joint configuration against altered external force in arm cranking.
Kinematic variances
In the cycling movement investigated here, each hand moved along a given path with a given velocity independently from the crank resistance. In particular, the hand moved on a 2-dimensional path (circle). The variance in hand position was not affected by crank resistance by definition. It was unknown, however, whether joint configuration variance would be affected by crank resistance. The considered system is in fact redundant because the intersegmental angles in the shoulder, elbow and wrist are changing during the movement while the hand follows a planar 2-dimensional trajectory. The range of angular motion of the shoulder elbow and wrist was 42.75°±0.63; 68.87° ±0.49 and 23.35° ±1.16 (mean ±SEM) respectively. As the system is redundant there exist infinite mapping from joint space to operational space to accomplish the task. Our results found that variances in angular changes in joints space are not affected by crank resistance. This was found for both arms. This suggests that during arm cycling, central control ensures stable movement execution at kinematic level even if crank resistance is altered. The kinematic requirements of the task do not vary for altered crank resistance, what changes is the additional effort necessary to execute the movement. This aspect suggests that when a mapping is chosen between joint space and operational space, it is maintained as the resistance at the crank increases. Furthermore, it provides evidence for the existence of an independent control of force and movement (Mason, 1981). The central nervous system (CNS) is able to handle two tasks separately. On one hand, it guarantees that the kinematic trajectory and velocity is executed. On the other hand, it is able to regulate the force the hand needs to apply without changing the kinematics, even though the kinematics and force generation are highly coupled through the non-linear dynamics of the neuro-mechanical system. The CNS thus parses muscular force for specific tasks, separately controlling the force necessary for the kinematics and the additional force required for the increasing crank resistance.
Studies on bimanual circle drawing tasks found that movements of the non-dominant arm were more variable than the movements of the dominant arm (Ryu and Buchanan, 2004). We did not find variance related differences between the arms in our experiments on constrained arm cranking movements. This may be explained by the fact that the hand path was fixed and the execution of the task did not require high dexterity. Future work will require to study variability of movements of the two arms in other constrained motor tasks and the relation of such variabilities to the dynamic-dominance hypothesis that was developed and applied for targeted reaching movements (Schaffer and Sainburg, 2017).
Muscle activation variances
Cycling against a higher crank resistance requires increased muscle activity. It is a general assumption that activation signals with higher amplitudes produce higher motor variances due to signal-dependent noise. It is unknown whether larger variances, observed when cranking was performed against higher crank resistance, are a consequence only of higher signal amplitudes or if other motor control factors also contribute. The magnitude of muscle activation variances was significantly affected by crank resistance. However, the shape of the variance curve did not depend on crank resistance (Fig. 5, Table 1).
Muscle activation variances during arm cranking increased with crank resistance while the resulting kinematic (angular) variances were unchanged. Our results support the idea that joint configuration variances, while cycling on an ergometer, are not affected by crank resistance and that during this motor task, neural control stabilizes joint configurations against altered external force. This conclusion held true for both arms. This suggests that the CNS is able to modulate separately a kinematic task and a force task.
A proportional variation of the muscle activation profiles as the crank resistance increases (and therefore a quadratic alteration of its variance) is possible only if the control system is linear. Given the nonlinearities of the dynamic system, such control can only occur if there is a prediction of the dynamic properties of the system and the CNS is capable of compensating the dynamic nonlinearity.
It has been shown that power output affected the corticospinal excitability of the biceps brachii and triceps brachii muscles during arm cycling (Spence 2016, Lockyer 2018). These studies show that corticospinal excitability is muscle dependent and suggest that the central command controlling different muscles may be different. However, this observation does not imply that muscles are controlled independently in arm cycling. Investigating combined activation signals of several muscles is a question of further research that may reveal features of central control of arm cycling. In the present exploratory study combined muscle activation was represented at each instant (t) by a vector (M(t)) of activations in a set of muscles (in particular by a 4-dimensional vector in which each coordinate related to the EMG amplitude of one arm muscle). Combined muscle activation profile incorporates all the considered muscles and investigating the variance of these activation profile assumes that muscles are controlled not independently and the result showed that this variance increased quadratically as crank resistance (and power output) increased. As stated above, this suggests that a control system that may control combined muscle activation is linear in arm cycling tasks. Our conclusion that movement and force may be controlled differently during arm cycling aligns with the assumption about another cyclic limb movement, namely that neural control of force output and kinematics (i.e. speed) may be differently controlled in lower limb cycling (Christensen 2000).
Limitations
We have analyzed different sources of kinematic variance. Variance could come from measurements errors from the instrumental setup; on the other hand, we have placed particular care on these aspects. Specifically, we have used a system that is able to measure the position of the limbs without direct contact and with submillimeter precision. Thus, we have avoided errors that can come from using systems like an encoder, where plays in the kinematic chain between hand and transducer via a transmission can affect the measurements. In our setup, measurements strictly depend on what the subject has performed and not from additional errors in the measurement chain. The precision of the ultrasound system we utilized is actually very high. Considering an average length segment all about 300 millimeters with an error of identification at the tip of each segment equal to 1 millimeter, the average angular error due to the measurement system is about 0.2 degrees. It can be seen that the standard deviation of the angular variance is much larger than that. Therefore, we can see that the variance of the joint angular displacement does not depend on the measurement errors but is strictly depending on the task. Considering the Uncontrolled Manifold Theory, we can speculate that there are infinite poses that can guarantee proper tracking of the handle along the circular trajectory. Thus, the subject is free to choose among every possible solution without compromising the kinematics of the endpoint.
Useful insights for rehabilitation
An aspect for rehabilitation practice that the present study provides is to help to plan proper upper body exercises for people with paraplegia, whose lower limbs are paralyzed. It is essential to prevent further health problems, which would be the consequence of a physically inactive lifestyle of people with paraplegia. Arm-cycling on arm-cycle ergometer offers them an excellent exercise which helps to enhance physical capacity and maintain stable movement execution when employing increased crank resistances during the series of training sessions. As the joint configuration variance is not affected by crank resistance, this motor task may involve a stable movement execution and may be well used in rehabilitation and training protocols. Another example of a potential application is functional electrical stimulation (FES) driven arm cycling for people with tetraplegia, who are unable to move the arm crank voluntarily (Zhou et al., 2018). When spinal cord injured individuals are not able to generate active muscle forces voluntarily, FES controlled arm cycling is a useful exercise. If muscle stimulation patterns are defined by observed muscle activity patterns of able-bodied individuals, then when crank resistance is increased during FES driven cranking, the stability of the control may be conserved. This may make the FES control easily adaptable to increased crank resistance.
Conclusions
In summary, we investigated arm cycling movements performed by able-bodied individuals on a cycle ergometer and addressed the question of how external load (crank resistance) affects the variances of joint configuration and muscle activation. The joint configuration variance was not affected by the crank resistance either in unimanual or bimanual cranking. This aspect was surprising because even though the hand path and cadence were constrained, a variability could be expected given that an increased resistance is associated to an increased motor noise that could have affected the time profile of the joint configuration variance.
Muscle activation variances increased quadratically with respect to the change in average muscle activation as the crank resistance increased, underlining a linear control. This observed kinematic, and muscle activity variances may reflect the separation of kinematic- and force-control. While a single controller based on the equilibrium point hypothesis was proposed in (Kolesnikov et al., 2011), more recent literature put forth the need for two separate controllers to compensate for dynamical forces (Mohan and Morasso, 2011). Our investigation suggests that the control scheme appears to allow a stable control of the constrained movement while independently compensating for the additional load and the effect of non-linear dynamics. Our experimental results are consistent with an operational space control scheme that decouples the kinematics and the dynamics (Khatib et al., 2018). As suggested in (Mason, 1981), the modulation of force could be accomplished by proper modulation of stiffness, which would not change the pose of the arm as a function of the load but simply compensate for the additional crank resistance. Besides the importance of the relation of kinematic and force control in an arm movement task in which the hand path is constrained, these results may be relevant for planning rehabilitative training procedures. The results suggest that arm cranking can be performed in a comfortable, stable manner when external load alters.